목차
관련 글 목록
- XAI - (1) 그래프를 이용한 방법 - PDP(Partial Dependence Plot)
- XAI - (2) 대리 모형(surrogate model)을 이용한 방법 - global surrogate model
- XAI - (3) 국소적 대리 모형(local surrogate model) - LIME(Local Interpretable Model-agnostic Explanations)
0. Recap
이전 글에서는 XAI의 개념과 필요성, 종류에 대해 간략하게 알아본 후 그래프를 이용한 귀납적 XAI 기법 중 하나인 PDP(Partial Dependence Plot)에 대해 알아보았다. PDP는 관심있는 변수를 제외한 다른 변수들의 값은 고정시킨 상태에서 관심있는 변수의 값만 특정 범위 안에서 변화시키며(일종의 시뮬레이션으로 볼 수 있음) 모형의 평균적인 예측 경향성을 파악하는 방법이다. 평균을 취하는 과정에서 변수간 상호작용이 가려질 수 있기 때문에 모든 관측치에 대한 시뮬레이션 정보를 표시하는 ICE plot을 그리기도 하고, 두개의 변수를 각각 x축과 y축에 표시한 후 색상의 차이로 예측값의 대소를 구분하여 등고선 그래프를 그리는 방법을 사용하기도 한다. PDP의 단점은 입력변수 사이의 상관관계가 강하게 존재하면 값을 변화시키는 그리드 내의 특정 데이터 포인트는 발생 가능성이 낮은 값이나 발생할 수 없는 값이 포함될 수 있다는 것이다. 이러한 문제점을 보완하기 위해 CPG(Conditional Predictive Graph)1나 ALE(Accumulated Local Effects) plot2 등이 기법이 제안되었다.
1. 대리 모형(surrogate model)이란?
이번 글에서는 또 다른 귀납적 XAI 기법 중 하나인 대리 모형(surrogate model)을 이용한 방법에 관해 살펴보려고 한다. 대리 분석 기법(Surrogate Analysis)은 엔지니어링 분야에서 사용되던 용어로 본래 기능을 흉내내는 간단한 대체재를 만들어 프로토타입이 동작하는지 판단하는 분석 방법이다. 실험설계 분야에서 많이 사용되는 반응 표면 분석법(Response Surface Methodology, RSM)도 대리 분석 기법 중 하나이다3. XAI에서 대리 분석은 복잡하고 설명하기 힘든 모형(블랙박스 모형)을 단순하고 설명하기 쉬운 모형(대리 모형)으로 대신 설명하는 방법을 말한다. 선형회귀 모형, 로지스틱 회귀모형, 트리모형 등의 설명 가능한 모형을 대리 모형으로 사용할 수 있다.
대리 모형은 학습시키는 방식에 따라 크게 두 가지 방향으로 분류해 볼 수 있다. train 데이터의 전부 또는 일부를 대리 모형으로 다시 학습하여 사용하는 방법을 전역적 대리 모형(global surrogate model)이라 하고, 특정 데이터 포인트 근방에서 샘플링된 데이터를 활용하여 대리 모형을 학습하여 사용하는 방법을 국소적 대리 모형(local surrogate model)이라고 한다. 이번 글에서는 전역적 대리 모형에 대해 다뤄보려고 한다.
2. 전역적 대리 모형(global surrogate model)
전역적 대리 모형(global surrogate model)은 블랙박스 모형을 학습시키는데 사용한 train 데이터의 전부 또는 일부를 설명 가능한 모형으로 다시 학습시켜서 블랙박스 모형을 설명하는 방식이다. 대리 모형이 블랙박스 모형의 예측패턴을 잘 모방할 수 있다면 블랙박스 모형이 어떻게 동작하는지에 관한 정보 없이도 블랙박스 모형을 설명할 수 있다고 보는 것이 전역적 대리 모형의 핵심 아이디어이다.
블랙박스 모형을 \(M\), 입력변수 데이터셋을 \(X_{n \times p}\), 타겟을 \(y_{n \times 1}\)라 하면, 전역적 대리 모형은 다음과 같은 방식으로 통해 얻을 수 있다.
1. \(X_{n \times p}\)와 \(y_{n \times 1}\)를 사용하여 블랙박스 모형 \(M\)을 학습시키고, 다시 \(X_{n \times p}\)를 이용하여 \(y_{n \times 1}\)에 대한 블랙박스 모형의 예측값 \(\hat{y}_{n \times 1}\)를 구한다.
2. 설명 가능한 모형 중 하나를 대리 모형으로 선택한 후, \(X_{m \times k}\)와 \(\hat{y}_{m \times 1}\)으로 대리 모형을 학습시킨다(\(m \le n, k \le p\)).
대리 모형을 학습시킬 때 관측치의 일부나 입력변수의 일부를 선택하여 사용하기도 한다. 불균형 클래스가 있는 분류 문제를 풀 때 언더샘플링을 적용하면 관측치의 일부만 사용하게 될 수 있다. 입력변수의 관점에서는 보통 상관계수가 높은 변수 중 하나만 남기는 작업을 수행하거나 L2 regularization을 활용하여 일부 변수만 선택하는 작업을 수행하기 때문에 전체 입력변수 중 일부만 사용하게 될 수 있다.
3. 대리 모형의 평가
전역적 대리 모형을 사용할 때의 가장 중요한 가정은 대리 모형이 블랙박스 모형의 예측 패턴은 잘 모방한다는 것이다. 그렇다면 대리 모형을 학습하여 블랙박스 모형 해석에 사용하기 전에 대리 모형이 정말 블랙박스 모형과 유사한 예측을 하는지 확인해 볼 필요가 있다. 대리 모형이 얼마나 블랙박스 모형과 유사한 예측을 하는지 평가하기 위해 사용할 수 있는 방법 중 하나는 \(R^2\)를 계산해보는 것이다. \(R^2\)는 다음과 같이 계산할 수 있다4:
$$R^2 = 1 - \frac{SSE}{SST} = 1 - \frac{\sum_{i=1}^{n}(\hat{y}_{*}^{(i)}-\hat{y}^{(i)})^2}{\sum_{i=1}^{n}(\hat{y}^{(i)}-\bar{\hat{y}})^2}$$
여기서 \(\hat{y}_{*}^{(i)}\)은 i번째 관측치에 대한 대리 모형의 예측값, \(\hat{y}^{(i)}\)는 블랙박스 모형의 예측값, \(\bar{\hat{y}}\)는 블랙박스 모형의 예측값의 평균이다. \(R^2\) 값이 1에 가까우면 대리 모형과 블랙박스 모형의 예측 결과가 유사하다는 의미이고, 이러한 경우에 대리 모형이 블랙박스 모형을 대신 설명하기 적합하다고 볼 수 있다.
4. 파이썬 코드
이번 글에서는 캐글의 IEEE-CIS Fraud Detection 데이터셋을 사용하여 예제 코드를 작성해보려고 한다.
https://www.kaggle.com/c/ieee-fraud-detection
IEEE-CIS Fraud Detection | Kaggle
www.kaggle.com
# 데이터 불러오기
import pandas as pd
train_id = pd.read_csv('train_identity.csv')
train_tr = pd.read_csv('train_transaction.csv')
# null 값이 없는 칼럼만 선택
n_null_train_id = train_id.isnull().sum()
n_null_train_tr = train_tr.isnull().sum()
train_id = train_id[list(n_null_train_id[n_null_train_id==0].index)]
train_tr = train_tr[list(n_null_train_tr[n_null_train_tr==0].index)]
# transaction 데이터와 identity 데이터 조인
X_train = pd.merge(train_tr.drop(columns=['isFraud']),
train_id, how='left', on='TransactionID')
y_train = train_tr.isFraud
# 조인 후 null 값이 있는 칼럼의 null 값을 0과 'NULL'로 채워줌
X_train['id_01'] = X_train['id_01'].fillna(0)
X_train['id_12'] = X_train['id_12'].fillna('NULL')
# 범주형 변수는 원핫인코딩, 연속형 변수는 mean-variance 스케일링
from sklearn.preprocessing import StandardScaler
def ohe(train, col):
from sklearn.preprocessing import OneHotEncoder
ohe = OneHotEncoder(sparse=False)
train_cat = ohe.fit_transform(train[[col]])
return pd.DataFrame(train_cat, columns=[col+ '_' + c for c in ohe.categories_[0]])
cat_cols = X_train.select_dtypes('O').columns.tolist()
X_train_num = X_train.select_dtypes('number').drop(columns=['TransactionID', 'TransactionDT'])
std_sc = StandardScaler()
X_train_scaled = pd.DataFrame(std_sc.fit_transform(X_train_num), columns= X_train_num.columns)
X_train_pp = pd.concat([X_train_scaled,
pd.concat([ohe(X_train[[col]], col) for col in cat_cols], axis=1)],
axis=1)예제 코드 작성을 위해 전처리는 최대한 간소화하여 진행하였다.
# LGB 모형 학습
from lightgbm import LGBMClassifier, plot_importance
mdl = LGBMClassifier()
mdl.fit(X_train_pp, y_train)먼저 LGB 모형을 디폴트 옵션으로 학습시킨 후 변수 중요도를 확인
from matplotlib import pyplot as plt
f, ax = plt.subplots(figsize=(6,6))
plot_importance(mdl, ax=ax);
이제 학습데이터에 대해 예측값을 구한 후 이를 대리 모형의 타겟으로 사용하여 Logistic Regression 모형을 학습시킨다. scikit-learn의 Logistic Regression 모형은 디폴트 설정이 L2 regularization을 적용하는 것으로 되어있다.
y_pred = mdl.predict(X_train_pp) # 대리 모형의 target 변수로 사용
# Logistic Regression 모형 학습
from sklearn.linear_model import LogisticRegression
surrogate = LogisticRegression(max_iter=1000)
surrogate.fit(X_train_pp, y_pred)대리 모형의 회귀계수를 확인해보면
df_coef = pd.DataFrame(surrogate.coef_[0], columns=['Coefficients'],
index=X_train_pp.columns).sort_values('Coefficients')
color = (df_coef.Coefficients>0).map({True: 'g', False: 'r'}).to_list()
df_coef['Coefficients'].plot.barh(color=color, figsize=(9,7))
plt.title('Surrogate model: Logistic Regression')
plt.axvline(x=0, color='.5')
plt.subplots_adjust(left=.3)
plt.xlabel('Coefficients')
plt.ylabel('Features');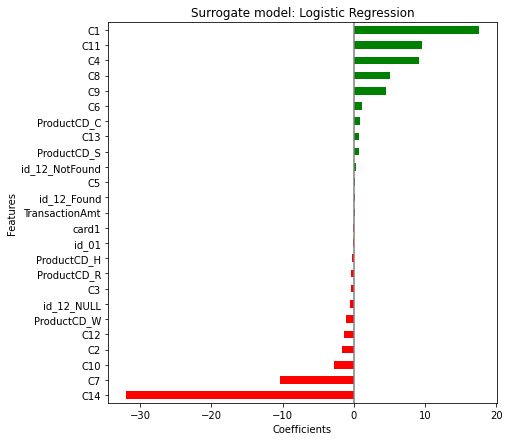
LGB 모형에서 변수중요도가 가장 높게 나온 card1 변수가 Logistic Regression 모형에서는 회귀계수의 절대값이 0에 가깝게 나온 것을 보면 두 모형의 예측결과가 상당히 다를 것 같은 느낌이 벌써부터 드는데, 대리 모형이 본 모형을 얼마나 잘 모방했는지 \(R^2\) 값을 구해보면
from sklearn.metrics import r2_score
lgb_prob = mdl.predict_proba(X_train_pp)[:, 1]
surrogate_prob = surrogate.predict_proba(X_train_pp)[:, 1]
r2_score(y_true=lgb_prob, y_pred=surrogate_prob)0.36813497445824406뭔가 0.7 이상은 나와야 비슷하게 대리 모형이 본 모형을 잘 모방한다고 볼 수 있을 것 같은데 0.36이면 모방을 잘 못하는게 아닌가 하는 느낌을 지울 수 없다. 이 부분이 대리 모형을 평가할 때 가장 애매한데, \(R^2\) 값을 기준으로 모형의 적합도를 판단할 때 항상 발생할 수 밖에 없는 문제이긴 하다. 블랙박스 모형을 완벽하게 모방하는 대리 모형을 기대하는 것보다는(그런 대리 모형이 있으면 처음부터 해석 가능한 모형을 사용하겠지) 해볼 수 있는 이런 저런 시도를 해보았을 때 가장 적합도가 높은 모형을 고르는 것이 현실적인 방안이라고 생각한다.
# 정상건을 일정비율로 언더샘플링
for ratio in [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]:
train_pp = pd.concat([X_train_pp, pd.Series(y_pred, name='TARGET')], axis=1)
train_pp0 = train_pp[train_pp.TARGET.isin([0])]
train_pp1 = train_pp[train_pp.TARGET.isin([1])]
train_sampled = pd.concat([train_pp1, train_pp0.sample(frac=ratio, random_state=42)], axis=0)
surrogate = LogisticRegression(max_iter=1000)
surrogate.fit(train_sampled.drop(columns=['TARGET']), train_sampled.TARGET)
from sklearn.metrics import r2_score
lgb_prob = mdl.predict_proba(X_train_pp)[:, 1]
surrogate_prob = surrogate.predict_proba(X_train_pp)[:, 1]
print(f'Undersampling rate: {ratio}, R2: {r2_score(y_true=lgb_prob, y_pred=surrogate_prob)}')Undersampling rate: 0.1, R2: -0.0746426800137312
Undersampling rate: 0.2, R2: 0.36608729467783874
Undersampling rate: 0.3, R2: 0.4443779247148323
Undersampling rate: 0.4, R2: 0.4502228884750604
Undersampling rate: 0.5, R2: 0.44100260576570216
Undersampling rate: 0.6, R2: 0.42314419797075964
Undersampling rate: 0.7, R2: 0.4111570055930832
Undersampling rate: 0.8, R2: 0.3973028729033681
Undersampling rate: 0.9, R2: 0.3818638617275104
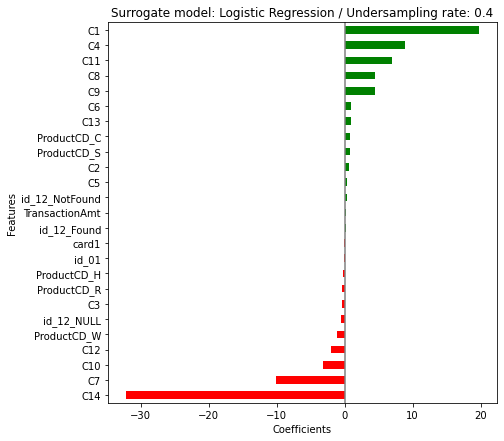
Undersampling rate: 1.0, R2: 0.36813497445824406정상건을 40%만 사용하여 대리 모형을 학습 시켰을 때 \(R^2\) 값이 가장 높게 나온다. 이 모형을 최종 대리 모형으로 사용하는 것을 고려해볼 수 있다.
- 허명회(2015), "기계학습 모형의 시각화, 통계연구(2015), 제20권 제 2호, 1-30" [본문으로]
- Apley, Daniel W., and Jingyu Zhu(2020), "Visualizing the effects of predictor variables in black box supervised learning models." Journal of the Royal Statistical Society: Series B (Statistical Methodology) 82.4(2020) [본문으로]
- 안재현(2020), "XAI 설명 가능한 인공지능, 인공지능을 해부하다", 위키북스, p.91 [본문으로]
- https://christophm.github.io/interpretable-ml-book/global.html [본문으로]

