XAI - (1) 그래프를 이용한 방법 - PDP(Partial Dependence Plot)

1. XAI(Explainable Artificial Intelligence)란 무엇인가?

XAI의 개념은 의사들의 부정확한 추론 과정을 확률적으로 모델링하는 방법을 제안한 Buchanan과 Shortliffe의 논문^[각주:1]에서 '설명 가능한 의사 결정 체계'라는 용어로 1975년에 처음 등장했다. XAI(Explainable Artificial Intelligence)라는 용어는 2004년에 Michel van Lent와 William Fisher, Michael Mancuso가 만든 이후 전문용어로 자리잡았다. 이들은 군대의 모의 전투 프로그램 속 NPC의 행동 이유를 설명하는 아키텍처를 제시했는데, 모의 전투의 상황을 벡터 형태로 출력하여 장교들이 모의 전투가 종료된 후에 상황을 분석하여 AI의 행동이유를 이해할 수 있게 하였다^[각주:2].

이후 다양한 형태의 XAI 기법에 관한 연구가 진행되었는데, 인터넷의 전신인 아르파넷(Arpanet), 스텔스기, GPS 등의 기술을 만들어낸 다르파(DARPA; Defense Advanced Research Project Agency)에서도 2016년 부터 XAI 프로젝트를 시작했다^[각주:3].
다르파의 XAI 프로젝트 메인 페이지에는 프로젝트의 개요와 목표 등이 소개되어 있고, 발표 슬라이드도 함께 첨부되어 있다.
https://www.darpa.mil/program/explainable-artificial-intelligence

다르파에서는 XAI 프로젝트의 목적을 아래와 같이 제시하고 있다.

Produce more explainable models, while maintaining a high level of learning performance (prediction accuracy); and
Enable human users to understand, appropriately trust, and effectively manage the emerging generation of artificially intelligent partners.

다르파의 프로젝트 목적에 언급된 것처럼 XAI는 모형의 예측결과를 사람이 이해할 수 있고 신뢰할 수 있게 하기 위한 기법의 총칭이라 할 수 있다.

프로젝트 일정을 보면 올해(2021년) toolkit 형태로 결과물이 나오는 일정으로 되어 있는데, 구글에 검색해보니 아직까지 공개된 결과는 없는 것으로 보인다.

2. XAI는 왜 필요한가?

해석가능성(interpretability)의 측면에서 볼 때 머신러닝 모형(RF, SVM, XGB, LGB, DNN, CNN 등등)과 선형모형의 가장 큰 차이점은 적합된 예측함수(fitted prediction function)에서 입력변수들이 예측결과를 만들어내는데 어떤 역할을 하는지 이해하기 어렵다는 점이다.
선형회귀(linear regression)나 로지스틱 회귀나 로지스틱 회귀(logistic regression) 같은 선형모형을 사용하면 아래와 같은 해석가능한(explainable) 예측함수를 얻을 수 있다.
$$f(x_1, \dots, x_p) = \hat{\beta_0} + \hat{\beta_1}x_1 + \dots + \hat{\beta_p}x_p$$
여기서 $x_1, \dots, x_p$는 입력변수, $\hat{\beta_0}, \dots, \hat{\beta_p}$는 추정된 회귀계수이다. 선형모형에서는 예측값(predicted value)을 만들어내는데 입력변수들이 기여하는 정도를 해당 변수의 계수 추정값을 통해 알 수 있다^[각주:4].
하지만, 머신러닝 모형의 예측함수는 선형모형의 예측함수처럼 파라미터 추정값과 입력변수의 선형결합 형태로 나타나지 않는다. 그래서 선형모형처럼 '다른 변수값이 동일할 때 특정변수의 값이 1단위만큼 변하면 예측값이 xxx만큼 변한다' 같은 설명이 불가능하다. 특정한 예측결과가 어떻게 나오게 되었는지 설명할 필요가 없는 경우라면 예측 성능만 신경쓰면 되겠지만, 사람들은 보통 왜 그런 예측값이 나왔는지 궁금해 한다.
예를 들어, 신용점수가 어느날 갑자기 100점 가까이 하락한 것을 확인한 직장인 A씨는 왜 본인의 신용점수가 하락했는지 궁금해할 수 있다. A씨가 신용점수를 제공하는 회사의 고객센터에 전화를 걸어 왜 자신의 신용점수가 갑자기 떨어졌는지 이유를 물어보았는데, 상담원이 '연체 확률을 높은 정확도로 예측하는 모형이 그렇게 판단했다' 같은 답변만 반복한다면 A씨는 매우 화가나서 금감원에 민원을 넣게 될 수 있다. 상담원이 'A씨의 전월 현금서비스 이용금액이 xx만원 이상이기 때문에 신용점수가 하락하였고, 상환 후 더 이상 현금서비스를 사용하지 않는다면 보통 n개월 후에 신용점수가 이전 상태로 회복된다' 같은 답변을 하는 것이 A씨의 궁금증을 좀 더 확실하게 해결해 줄 수 있는 방법이다.

3. XAI 기법의 종류

DARPA에서는 XAI 기법을 세 가지로 분류하여 제시하고 있다.

(1) Deep Explanation(딥러닝 설명 모델)

Microsoft의 Bonsai 프로젝트에서는 Deep Explanation을 아래의 세 가지 키워드로 요약하고 있다.

Learning Semantic Associations
Generating Visual Explanations
Rationalizing Neural Predictions

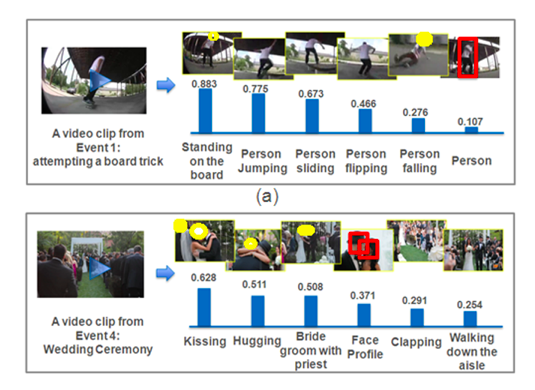
딥러닝 쪽은 자세히 파본적이 없어서 정확히 무엇을 하는지는 모르겠으나 슬라이드에 나온 설명과 Bonsai 블로그에 나온 내용을 종합해보면, 특정한 목적을 가진 해석가능한 변수를 딥러닝 모형으로 학습시켜서 사용하자! 인 것 같다. 블로그에서는 비디오의 특정 장면을 설명하기 위해 관련된 사건이 얼마나 발생했는지 카운팅 하는 것을 예시로 제시하고 있다.

(2) Interpretable Models(해석가능한 모형)

대표적인 해석가능한 모형의 목록은 다음과 같다^[각주:5].

Linear Regression
Logistic Regression
GLM, GAM
Decision Tree
Decision Rules
RuleFit

요약하면 전통적인 통계 모형들과 디시전 트리의 다양한 변형. 참고로, RuleFit은 GBM 논문(Greedy function approximation: a gradient boosting machine)으로 유명한 Jerome H. Friedman이 만든 방법인데 변수 간 상호작용을 탐지하는데 주안점을 둔 방법이다. 이번 글에서 소개할 PDP(Partial Dependence Plot)도 Friedman이 'Greedy function approximation: a gradient boosting machine' 논문에서 제안한 방법론이다.

(3) Model Induction(귀납적 모델)

최근에 나오는 XAI 방법론들은 귀납적 모델 분류에 속하는 것들이 많다. PDP나 ICE(Individual Conditional Expection) plot 같은 그래프를 이용한 방법이나 LIME 같은 surrogate model(대리 모형)을 이용한 방법 등이 여기에 속한다. 이러한 방법론들은 model agnostic method(모델의 종류에 관계없이 사용가능한 방법)이기 때문에 자주 사용된다.

4. XAI 기법을 활용할 때 주의해야 할 점

머신러닝 모형을 설명하기 위한 XAI 기법을 사용할 때 유념해야하는 것이 있다. XAI 기법은 현상에 대한 모형의 예측을 설명하기 위한 것이지 현상 자체를 설명하기 위한 것이 아니며, 인과적 추론을 위해서는 도메인 지식을 기반으로 한 통제된 실험이 수반되어야 한다는 것이다. XAI 기법으로 모형을 해석하여 입력변수 x1이 증가할수록 타겟변수 y의 예측값이 증가한다는 결과를 보았을 때, 'x1을 증가시키면 y를 증가시킬 수 있다'와 같은 해석을 하지 않도록 주의해야 한다. 자세한 내용은 아래 글들을 참고해보면 좋을 것 같다.

https://brunch.co.kr/@gimmesilver/54

실전 이탈 예측 모델링을 위한 세 가지 고려 사항 #2

실전 이탈 예측 모델링을 위한 세 가지 고려 사항 #1 2. Concept drift 는 모델링 전반에 걸쳐 고려해야할 문제이다. 실전에서 예측 모델을 서비스에 적용해 본 분이라면 예측 모델이 처음에는 잘 맞

brunch.co.kr

https://brunch.co.kr/@gimmesilver/68

도메인 지식이 결여된 인과 추정이 위험한 이유

시작하며 간혹 '데이터 분석가에게 도메인 지식이 필요한가?' 에 대한 질문을 받거나 관련된 논의글을 보곤 합니다. 전 도메인 지식이 필요할 뿐만 아니라 도메인 지식이 없는 상태에서 데이터

brunch.co.kr

https://benheo.github.io/2021/08/28/why_do_we_learn_causal_inference

[Product 시리즈 1] 프로덕트 분석가가 인과추론을 공부하면 좋은 이유 - Freak Analyst

나에게 온 한 통의 문자 얼마 전 VIBE에서 이런 문자가 왔습니다. 문자 내용을 확인해보니 파티룸 기능(노래 들으면서 클럽하우스처럼 얘기하는 기능)이 추가되면서 기존 이탈 유저를 복귀시키기

benheo.github.io

5. PDP(Partial Dependence Plot)

이번 글에서는 그래프를 이용한 가장 기본적인 XAI 기법 중 하나인 PDP(Partial Dependence Plot, 편의존성 플롯^[각주:6])에 관해 살펴보려고 한다. PDP는 앞서 언급한 것처럼 Jerome H. Friedman이 'Greedy function approximation: a gradient boosting machine'에서 제안한 방법론이다. 편의존성을 계산하는 방법은 편도함수나 편회귀계수를 구하는 방법과 개념적으로 유사하다. 편의존성은 관심있는 특정 입력변수를 제외한 다른 입력변수들의 값은 고정시킨 상태(상수 취급)에서 관심있는 입력변수의 값을 변화시키며(변수 취급) 예측값을 계산한 후, 그 값들의 평균을 낸 것이다. 관심있는 입력변수의 값을 변화시키는 범위는 해당 변수의 최솟값과 최댓값 사이로 하고, 보통 일정 간격으로 그리드를 만들어 사용한다. 입력변수 값의 그리드를 x축에 표시하고, 이 값을 넣어 계산된 편의존성 값을 y축에 표시하여 PDP를 그릴 수 있다. 이를 수식으로 표현하면 다음과 같다^[각주:7].

편의존성(partial dependence, PD)의 정의 (Friedman, 2001):

$j=1,\dots,p$에 대하여, 입력변수 $x_j$의 편의존성은
$$\bar{f}_j(t)=\frac{1}{n}\sum_{i=1}^{n}{f(x_{i1}, \dots, t, \dots, x_{ip})}$$
로 정의된다. 여기서 $x_{i1}, \dots, x_{ip}$는 입력변수 $x_1, \dots, x_p$의 $i$번째 관측값이고, $f$는 예측함수이다. 편의존성을 입력변수 $x_j$의 최솟값과 최댓값 사이에서 계산한 후, 2차원 그래프로 나타낸 것이 PDP이다.
$$\{ (t, \bar{f}_j(t)) | \min_{i=1,\dots,n}(x_{ij}) \le t \le \max_{i=1,\dots,n}(x_{ij}) \}$$

이제 파이썬 코드를 통해 PDP를 어떻게 구현하는지 알아보자.

import pandas as pd 
import numpy as np 
from sklearn.datasets 
import load_boston 
from sklearn.ensemble import RandomForestRegressor 
from sklearn.inspection import plot_partial_dependence 
from sklearn.inspection import partial_dependence 
from matplotlib import pyplot as plt 

boston = load_boston() 
boston.keys() 
# dict_keys(['data', 'target', 'feature_names', 'DESCR', 'filename']) 

X = pd.DataFrame(boston['data'], columns=boston['feature_names']) 
y = boston['target']

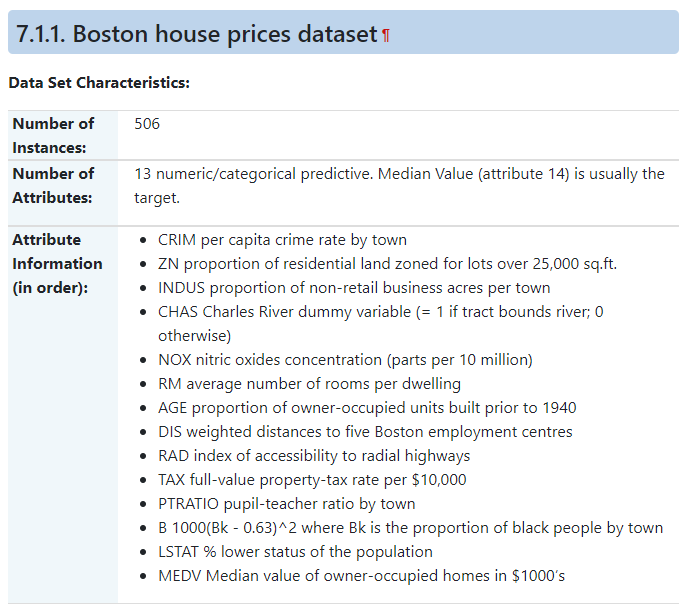
이번 글에서는 사이킷런 데이터셋에 있는 보스턴 집값 데이터를 이용해보려고 한다. 데이터를 불러온 후 랜덤포레스트 모델을 학습한다.

model = RandomForestRegressor(n_estimators=100, random_state=0) model.fit(X, y)

sklearn.inspection에 있는 plot_partial_dependence 함수를 이용하여 PDP를 그릴 수 있다.

grid_resolution: 그리드에 몇 개의 관측치를 포함시킬 것인지
percetiles: 그리드를 feature(여기서는 LSTAT)의 어떤 범위에서 생성할 것인지. (0, 1)이면 [최솟값, 최댓값]
kind='average', method='brute' 일 때 위에서 설명한 정의와 동일한 계산을 수행

#### PDP for LSTAT #### 
fig, ax = plt.subplots(figsize=(6, 6))
plot_partial_dependence(estimator=model, X=X, features=['LSTAT'], 
                        grid_resolution=round(X.shape[0]*0.1), percentiles=(0, 1), 
                        kind='average', method='brute',
                        ax=ax);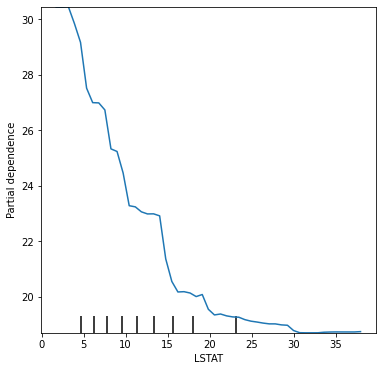

LSTAT에 대한 PDP를 그려보면 LSTAT 값이 증가할수록 편의존성 값이 감소하는 형태를 보인다는 것을 알 수 있다. 이는 여기서 학습시킨 랜덤포레스트 모형이 LSTAT 값이 증가할수록 집 값을 더 낮게 예측한다는 것을 알 수 있다. X축 위에 보이는 까만 새로줄은 'rug'라고 하는데 PDP 만으로는 LSTAT의 데이터 분포를 알 수 없기 때문에 실제 LSTAT 값이 분포하는 위치를 표시해주는 것이다.

X.LSTAT.plot.hist(figsize=(6,6), alpha=0.5);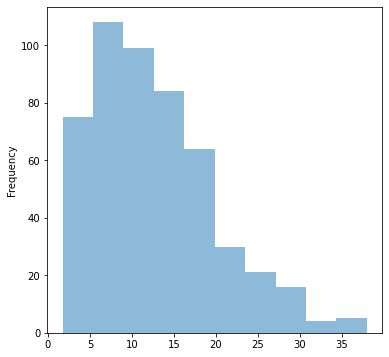

LSTAT의 히스토그램을 참고해보면 rug는 데이터 밀도가 높을수록 좁은 간격으로 표시되고, 데이터 밀도가 낮을수록 넓은 간격으로 표시된다는 것을 알 수 있다.

sklearn.inspection에 있는 partial_dependence 함수를 이용하면 편의존성 값과 그리드 정보를 얻을 수 있다. 'average'에 있는 값이 편의존성 값이고, 'values'에 있는 값이 최솟값과 최댓값 사이에서 만들어진 그리드 값이다.

res = partial_dependence(estimator=model, X=X, features=['LSTAT'], 
                         grid_resolution=round(X.shape[0]*0.1), percentiles=(0, 1), 
                         kind='average', method='brute')
res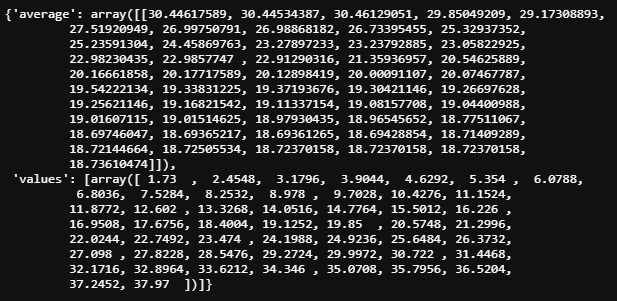

min(X.LSTAT), max(X.LSTAT) 
# (1.73, 37.97)

이를 직접 구현해보면 다음과 같다.

grid = res['values'][0]
_partial_dependence = [0 for i in range(len(grid))]
for i in range(round(X.shape[0]*0.1)):
    X_new = X.copy()
    X_new['LSTAT'] = grid[i] # 다른 변수값들은 그대로 두고, LSTAT 값만 변화시킴
    pred = model.predict(X_new)
    _partial_dependence[i] = np.mean(pred)
    
np.round(np.array(_partial_dependence), 8)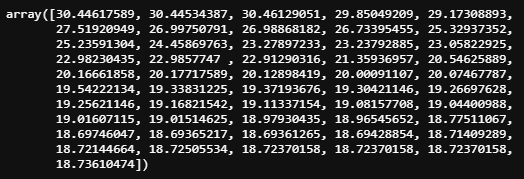

plt.figure(figsize=(6,6))
plt.plot(res['values'][0], _partial_dependence)
plt.xlabel('LSTAT')
plt.ylabel('Partial Dependence');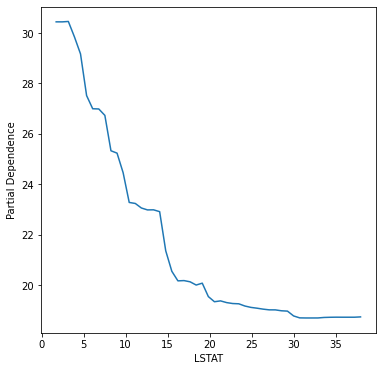

LSTAT과 MEDV(y)의 산점도를 함께 그려서 비교해보면

plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.plot(res['values'][0], _partial_dependence)
plt.xlabel('LSTAT')
plt.ylim((0, 52))
plt.xlim((0, 39))
plt.ylabel('Partial Dependence')

plt.subplot(1,2,2)
plt.scatter(X.LSTAT, y, alpha=0.5)
plt.xlabel('LSTAT')
plt.ylabel('MEDV');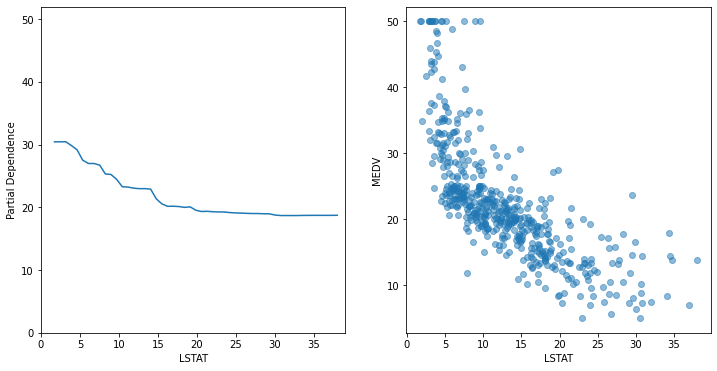

관측치별 예측값의 평균을 구한 것이기 때문에 partial dependence 값은 LSTAT의 각 지점에서 y값의 평균 근처에 모여 있는 것을 볼 수 있다.

PDP를 특정 입력변수 값의 변화에 따른 예측값의 평균적인 변화를 관찰할 수 있다는 장점이 있다. 하지만 평균을 구하는 과정에서 상호작용(interaction)의 존재 같은 데이터의 특성이 함께 뭉게질 수 있다는 단점이 있다. 평균을 구하지 않고 고 그리드 값의 변화에 따른 모든 관측치의 예측값을 그래프에 표시하는 방법이 ICE Plot(Individual Conditional Expectation Plot)이다.

fig, ax = plt.subplots(figsize=(6, 6))
plot_partial_dependence(estimator=model, X=X, features=['LSTAT'], 
                        grid_resolution=round(X.shape[0]*0.1), percentiles=(0, 1), 
                        kind='individual', method='brute',
                        ax=ax)
plt.plot(res['values'][0], _partial_dependence, color='red');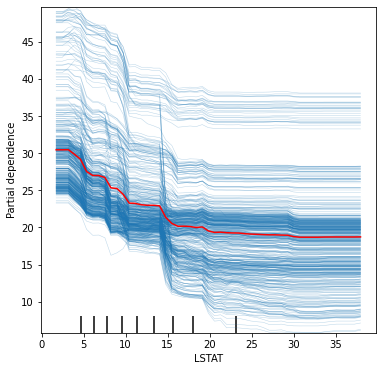

plot_partial_dependence 함수에서 kind='individual'로 설정하면 ICE Plot을 그릴 수 있다. ICE Plot은 보통 Partial Dependence를 함께 표시하여 사용한다^[각주:8]. LSTAT 변수는 모든 관측치가 대체로 일관된 패턴을 보이는 것을 알 수 있고, LSTAT변수를 다른 변수와 상호작용이 존재하지 않을 가능성이 높아보인다.

fig, ax = plt.subplots(figsize=(6, 6))
plot_partial_dependence(estimator=model, X=X, features=['RM'], 
                        grid_resolution=round(X.shape[0]*0.1), percentiles=(0, 1), 
                        kind='individual', method='brute',
                        ax=ax)
res = partial_dependence(estimator=model, X=X, features=['RM'], 
                         grid_resolution=round(X.shape[0]*0.1), percentiles=(0, 1), 
                         kind='average', method='brute')
plt.plot(res['values'][0], res['average'][0], color='red');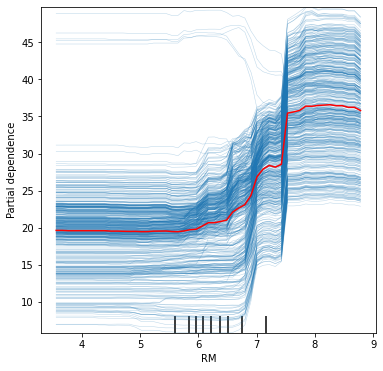

RM 변수에 대한 ICE plot의 좌측 상단을 보면 일부 관측치들이 나머지 관측치들과는 다른 패턴을 보임을 알 수 있다. 보통 이렇게 선들이 교차하는 패턴을 보이는 변수들에서 다른 변수들과의 상호작용이 존재할 가능성이 있다. RM 변수의 경우 패턴을 벗어나는 관측치들이 많지 않고 RM 값이 커질수록 예측값도 함께 커지는 경향성이 훨씬 강하여 다른변수와의 유의한 상호작용은 나타나지 않을 것으로 보이긴 한다. X자 패턴이 강하게 보이는 변수일수록 상호작용이 유의하게 나타날 가능성이 높다.

fig, ax = plt.subplots(figsize=(6, 6))
plot_partial_dependence(estimator=model, X=X, features=[('RM', 'LSTAT')], 
                        grid_resolution=round(X.shape[0]*0.1), percentiles=(0, 1), 
                        kind='average', method='brute',
                        ax=ax);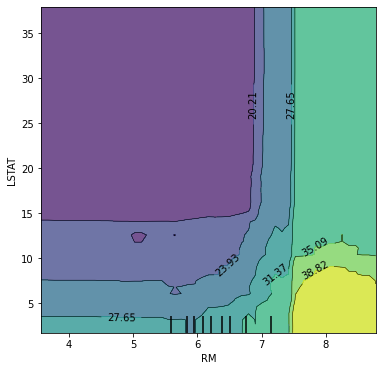

features에 튜플로 두 개의 변수를 넣어주면 등고선 형태로 2차원 PDP를 그려주는데, 예측값의 크기는 색상의 차이로 표현된다. 위의 그래프를 통해 이 모형은 LSTAT 값이 작고 RM 값이 클수록 집 값을 크게 예측하는 것을 알 수 있다. 또한, (LSTAT > 15) and (RM < 7) 인 경우에는 평균적인 예측값의 변화가 거의 없지만, 그 이외의 영역에서는 예측값의 변화가 더 큰 것을 알 수 있다.

지금까지는 연속형 변수의 PDP를 그려보았는데, 범주형 변수의 경우 그리드 값을 범주형 변수의 각 항목으로 볼 수 있기 때문에 각 항목에 대해 partial dependence를 계산하며 막대그래프를 그려주면 된다. 보스턴 데이터의 CHAS(강의 경계에 있으면 1 아니면 0) 변수에 대한 PDP를 그려보면

# CHAS 변수는 더미코딩 되어 있음
res = partial_dependence(estimator=model, X=X, features=['CHAS'], 
                         grid_resolution=2, percentiles=(0, 1), 
                         kind='average', method='brute')
df = pd.DataFrame(dict(partial_dependece=res['average'][0]), index=res['values'][0].astype(int))
df.plot.bar(figsize=(6,6), rot=0)
plt.ylim((0,30))
plt.xlabel('CHAS');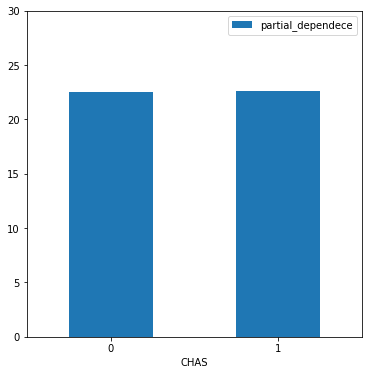

강의 경계에 있는지 여부는 모형의 예측값을 크게 변화시키지 않는 것으로 보인다.

ICE를 계산하여 박스플롯을 그려볼 수도 있다.

# CHAS 변수는 더미코딩 되어 있음
res = partial_dependence(estimator=model, X=X, features=['CHAS'], 
                         grid_resolution=2, percentiles=(0, 1), 
                         kind='individual', method='brute')
ice = res['individual'][0]
df = pd.DataFrame(dict(CHAS_0=ice[:,0], CHAS_1=ice[:,1]), index=range(len(ice)))
df.boxplot(figsize=(6,6));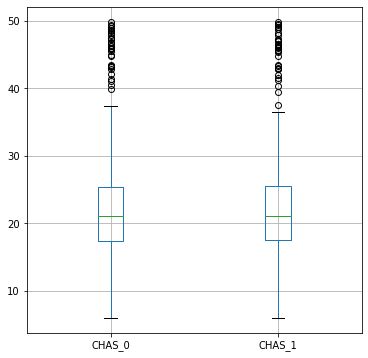

6. 글을 마치며

이번 글에서는 XAI의 개념과 필요성, XAI 기법의 종류를 살펴보았고, 그래프를 이용한 가장 단순하고 오래된 방법인 PDP에 대해 알아보았다. PDP를 그리면 모형의 평균적인 예측 경향성을 한눈에 알아볼 수 있다는 장점이 있지만 변수 간 상호작용이 존재해도 이를 파악할 수 없다는 단점이 있다. 그래서 PDP를 평균내지 않고 그대로 보는 ICE plot나 2차원 PDP를 그려서 모형이 변수 간 상호작용을 탐지하는지 파악해보기도 하고, Centered ICE plot, Derivative ICE plot 등의 기법을 활용하기도 한다. PDP의 단점은 입력변수 사이의 상관관계가 강하게 존재하면 값을 변화시키는 그리드 내의 특정 데이터 포인트는 발생 가능성이 낮은 값이나 발생할 수 없는 값이 포함될 수 있다는 것이다. 이러한 문제점을 보완하기 위해 CPG(Conditional Predictive Graph)^[각주:9]나 ALE(Accumulated Local Effects) plot^[각주:10] 등의 기법이 제안되었다.
나의 석사논문은 CPG를 그리는 방향을 다차원으로 확장하는 것이다. 기존 방법론들이 그래프를 그릴때 각 변수 축 방향의 벡터에 예측함수를 projection하는 방식이라면 석사논문에서 제안한 방법은 특정한 p차원의 방향벡터(ex. 회귀계수 벡터, 주성분 벡터)에 예측함수를 projection하는 것이다. p차원 방향벡터의 의미를 어떻게 해석할 것인지가 디펜스 할 때까지 최대 난제였는데, 깔끔한 해결책은 찾지 못한채로 마무리 하였다. 개인적으로는 선형회귀모형이나 로지스틱 회귀모형의 회귀계수 방향으로 CPG를 그려보았을 때 선형성이 어느 정도로 나타나는지 시각적으로 확인해 볼 수 있는 방법을 제시했다는 의의를 두고 싶다.
그래프를 이용한 방법에 대해 글에서 다루지 못한 내용들은 참고자료를 보면 채워질 것으로 생각한다. 특히, 참고자료 (1), (2)는 XAI에 관심이 있는 사람이라면 반드시 읽어봐야 할 책이라고 생각한다. (1)은 Python, (2)는 R 코드를 기반으로 설명하는 책이다.
PDP를 그리기 위해 사이킷런에 있는 함수들을 사용하였는데, pdpbox 패키지를 활용하면 더 깔끔하고 디테일한 그래프를 그려볼 수 있다.

7. 참고자료

(1) XAI 설명 가능한 인공지능, 인공지능을 해부하다 - 블랙박스를 이해하고 시스템의 신뢰성을 높이기 위한

XAI 설명 가능한 인공지능, 인공지능을 해부하다 - YES24

XAI(eXplainable Artificial Intelligence)는 인공지능의 판단 이유를 설명하는 연구 분야로, 인공지능 기술이 확대되면서 그 필요성이 함께 증가하고 있다. 이것은 알고리즘의 설계자조차 인공지능의 판단

www.yes24.com

(2) Interpretable Machine Learning

Interpretable Machine Learning

Machine learning algorithms usually operate as black boxes and it is unclear how they derived a certain decision. This book is a guide for practitioners to make machine learning decisions interpretable.

christophm.github.io

(3) Interpretable Machine Learning 번역자료

Chapter 1. Introduction

이 책은 여러분에게 (지도학습 방법의) 기계학습 모델을 해석할 수 있는 방법을 알려주는 책입니다. 이후 소개될 chapter들에서는 몇몇 수학적 수식이 포함되어있지만 수식을 모두 이해하지는 못

tootouch.github.io

(4) 정회빈(2019), 지도학습 예측모형의 시각화, 국내석사학위논문 고려대학교 대학원

http://www.riss.kr/search/detail/DetailView.do?p_mat_type=be54d9b8bc7cdb09&control_no=0508ab4f89b6028fffe0bdc3ef48d419

www.riss.kr

(5) The R Journal에 실린 pdp 패키지 소개 자료 번역

RPubs - pdp: An R Package for Constructing Partial Dependence Plots

rpubs.com

(6) https://scikit-learn.org/stable/modules/partial_dependence.html

4.1. Partial Dependence and Individual Conditional Expectation plots — scikit-learn 0.24.2 documentation

4.1. Partial Dependence and Individual Conditional Expectation plots Partial dependence plots (PDP) and individual conditional expectation (ICE) plots can be used to visualize and analyze interaction between the target response and a set of input features

scikit-learn.org

Shortliffe, Edward H, and Bruce G. Buchanan (1975), "A model of inexact reasoning in medicine." Mathematical biosciences 23.3-4: p.351-379 [본문으로]
안재현(2020), "XAI 설명 가능한 인공지능, 인공지능을 해부하다", 위키북스, p.3-4 [본문으로]
안재현(2020), "XAI 설명 가능한 인공지능, 인공지능을 해부하다", 위키북스, p.2 [본문으로]
정회빈(2019), "지도학습 예측모형의 시각화", 국내석사학위논문 고려대학교 대학원 [본문으로]
https://christophm.github.io/interpretable-ml-book/simple.html [본문으로]
PDP를 '부분 의존성 플롯'으로 번역하는 경우가 많은데, partial derivative를 '편도함수(偏導函數)', partial regression coefficient를 '편회귀계수(偏回歸係數)'라고 번역하는 것과 같은 맥락에서 partial dependence를 편의존성(偏依存性)으로 번역하는 것이 적절하다고 본다. [본문으로]
정회빈(2019), "지도학습 예측모형의 시각화", 국내석사학위논문 고려대학교 대학원 [본문으로]
kind='both'로 설정하면 같이 표시가 되는데 같은 색상으로 표시되어 구분이 되지 않아 따로 그려줌 [본문으로]
허명회(2015), "기계학습 모형의 시각화, 통계연구(2015), 제20권 제 2호, 1-30" [본문으로]
Apley, Daniel W., and Jingyu Zhu(2020), "Visualizing the effects of predictor variables in black box supervised learning models." Journal of the Royal Statistical Society: Series B (Statistical Methodology) 82.4(2020) [본문으로]

저작자표시 비영리