[백테스팅] 정적자산배분 - (3) 영구 포트폴리오(Permanent Portfolio)
관련 글 목록
1. 들어가며
이번 글에서는 해리 브라운(Harry Browne)이 만든 자산배분 전략인 영구 포트폴리오(Permanent Portfolio)에 대해 정리해보려고 한다. 해리 브라운은 미국의 작가이자 정치인1이자 투자 자문가로, 그의 저서 <Fail-Safe Investing: Lifelong Financial Security in 30 Minutes>에 영구 포트폴리오의 개념이 제시되어 있다.

영구 포트폴리오는 주식, 채권, 금, 현금(또는 단기국채(treasury bill))에 동일 비중으로 자산을 배분하는 전략으로, 어떤 경제상황에서도 영구적으로 사용할 수 있다는 의미에서 붙여진 이름이다. Investopedia에서 영구 포트폴리오의 정의에 관해 검색해보면 다음 같이 핵심 요약이 되어 있다.
- The objective of a permanent portfolio is to perform well in any economic condition through diversity.
- A permanent portfolio is composed of equal parts stocks, bonds, gold, and cash.
- Historical performance has shown a permanent portfolio to perform well in the long-term but not as well as a traditional 60/40 stock-bond portfolio.
- The advantage is that a permanent portfolio reduces losses in market downturns, which may be beneficial for certain investors.
벤치마크로 사용되는 60/40 포트폴리오 보다 기대 수익률은 떨어지지만 시장 하락기에 적게 잃는 전략이라는 게 영구 포트폴리오의 핵심으로 보인다.
2. 영구 포트폴리오(Permanent Portfolio) 백테스팅
아래 표는 <거인의 포트폴리오>에 제시된 영구 포트폴리오의 백테스팅 결과이다. 책에 제시된 백테스팅 결과는 Allocate Smartly에서 가져온 것으로 보인다.
거인의 포트폴리오(강환국) p.163-p.167
| 투자전략 | 영구 포트폴리오 |
| 기대 연복리수익률 | 8% 정도 |
| 포함자산 | 미국주식(SPY), 미국 장기국채(TLT), 금(GLD), 미국 초단기채권(BIL) |
| 매수전략 | 4개 ETF에 자산을 4등분 |
| 매도전략 | 연 1회 리밸런싱 |
영구 포트폴리오의 주요 지표(1970.1~2021.8)
| 포트폴리오 | 초기자산 (달러) |
최종자산 (달러) |
연복리 수익률(%) |
표준편자 (%) |
수익 난 월 (%) |
MDD (%) |
샤프비율 |
| 영구 포트폴리오 |
10,000 | 762,322 | 8.8 | 7.2 | 65.0 | -12.7 | 0.57 |
이제 백테스팅에 필요한 라이브러리와 데이터를 불러와보자. 과거 데이터(historical data)는 야후 파이낸스에서 제공하는 데이터를 사용하였고, yfinance 패키지를 이용하여 가져왔다. 가격 데이터는 수정 종가(adjusted close)이다.
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
IPython_default = plt.rcParams.copy()
import yfinance as yf
import pyfolio as pf
import quantstats as qs
tickers = ['SPY', 'TLT', 'GLD', 'BIL', 'IEF']
df_close = yf.download(tickers=tickers,
period='max',
interval='1d',
auto_adjust=True # True: adjust all OHLC automatically
)['Close'][tickers]
print('Start date of each stock')
print('-'*25)
for ticker in tickers:
print(f"{ticker}: {df_close[[ticker]].dropna().iloc[0].name.strftime('%Y-%m-%d')}")
print('-'*25)
Start date of each stock
-------------------------
SPY: 1993-01-29
TLT: 2002-07-30
GLD: 2004-11-18
BIL: 2007-05-30
IEF: 2002-07-30
-------------------------BIL(미국 단기국채)의 데이터가 2007년 5월 30일 부터 존재하는데, 현금성 자산을 BIL로 넣은 것이므로, 백테스팅 기간을 조금 더 확보하기 위해 현금보유(CASH)라고 가정하고 백테스팅을 진행하였다. 60/40 포트폴리오를 벤치마크로 하여 성과를 비교하기 위해 IEF 데이터도 불러와 주었다.
df_close['CASH']=1
tickers = ['SPY', 'TLT', 'GLD', 'CASH']
df = df_close[tickers].dropna()
"""
define trading period
time_period: dataframe converted from datetime index of price dataframe
traiding_period: dataframe contains start_date and end_date of trading
+ resampled from time_period to yearly frequency and last business day of a month
+ last day of time_period assigned to last end_date
"""
time_period = df.index.to_frame()
trading_period = time_period.resample('BM').last().iloc[::12, :].rename(columns={'Date':'start_date'})
trading_period = trading_period.assign(end_date=trading_period.start_date.shift(-1).fillna(time_period.iloc[-1].name))
trading_period
def get_mdd(df_price, start, end, col):
"""
generates maximum drawdown(MDD) of asset prices
MDD: the maximum observed loss from a peak to a trough of a portfolio, before a new peak is attained
Parameters
----------
df_price: pd.DataFrame
dataFrame with datetime index and (adjusted) close prices
example:
----------------------------------------------------
SPY IEF
Date
2002-07-30 61.6628 46.0411
2002-07-31 61.8120 46.4633
... ... ...
2022-09-15 388.5240 98.6000
2022-09-16 385.5600 98.6800
----------------------------------------------------
start: datetime
trading start date
example: Timestamp('2004-11-30 00:00:00')
end: datetime
trading end date
example: Timestamp('2005-11-30 00:00:00')
col: str
The column name of the cumulative return of the asset for which MDD is to be calculated
Return
----------
return: pd.Series
Series of MDD for the trading period
"""
# select data within the trading period
df_price = df_price[start:end].copy()
return ((df_price[col]-df_price[col].cummax())/df_price[col].cummax()).cummin()
def get_pf_returns(df_price, tickers, start, end, weights=None, use_signal=None):
"""
generates portfolio returns
Parameters
----------
df_price: pd.DataFrame
dataFrame with datetime index and (adjusted) close prices
example:
----------------------------------------------------
SPY IEF
Date
2002-07-30 61.6628 46.0411
2002-07-31 61.8120 46.4633
... ... ...
2022-09-15 388.5240 98.6000
2022-09-16 385.5600 98.6800
----------------------------------------------------
tickers: list
list of tickers
example: ['SPY', 'IEF']
start: datetime
trading start date
example: Timestamp('2004-11-30 00:00:00')
end: datetime
trading end date
example: Timestamp('2005-11-30 00:00:00')
weights: list, optional
list of weights. if weights is None, equal weights are assumed
example: [0.6, 0.4]
use_signal: Boolean, optional
True/False. if True is assigned, buy signal is used. #### future work
Return
----------
return: pd.DataFrame
prices, daily returns, cumulative returns, MDD for each asset and the portfolio
example:
----------------------------------------------------
SPY IEF SPY_RET IEF_RET PF_RET SPY_CUMRET IEF_CUMRET PF_CUMRET SPY_MDD IEF_MDD PF_MDD
Date
2002-07-31 0.0000 0.0000 0.0000 0.0000 0.0000 1.0000 1.0000 1.0000 0.0000 0.0000 0.0000
2002-08-01 60.1982 46.6548 -0.0261 0.0041 -0.0110 0.9739 1.0041 0.9890 -0.0261 0.0000 -0.0110
2002-08-02 58.8489 47.0152 -0.0224 0.0077 -0.0073 0.9521 1.0119 0.9817 -0.0479 0.0000 -0.0183
... ... ... ... ... ... ... ... ... ... ... ...
2003-07-30 68.3896 49.3867 -0.0024 0.0080 0.0028 1.1064 1.0629 1.0959 -0.1886 -0.0743 -0.0733
2003-07-31 68.5482 49.0572 0.0023 -0.0067 -0.0022 1.1090 1.0558 1.0936 -0.1886 -0.0743 -0.0733
----------------------------------------------------
"""
# define weights
if weights is None:
weights = [1/len(tickers) for _ in range(len(tickers))]
# calculate daily returns
ret_dict = {f'{ticker}'+'_RET': df_price[ticker].pct_change().fillna(0) for ticker in tickers}
df_price = df_price.assign(**ret_dict)
# select data within the trading period
df_trade = df_price.loc[start:end].copy()
# assign 0 for the first row. returns cannot be calculated on the first trading day
df_trade.loc[start, :] = 0
#### future work
"""
if use_signal==True:
df_sig = pd.concat([df_trade.index.to_frame().drop(columns=['Date']),
df.loc[[start], sig_dict.keys()]
], axis=1).ffill()
df_sig.columns = tickers
df_trade = df_trade.assign(**{col: df_trade[col]*df_sig[col] for col in tickers})
else:
df_trade = df_trade.assign(**{col: df_trade[col] for col in tickers})
"""
# calculate daily portfolio returns
df_trade = df_trade.assign(PF_RET=df_trade[ret_dict.keys()].dot(weights))
# calculate cumulative returns within the trading period
cumret_dict = {f'{col}_CUMRET': (1+df_trade[f'{col}_RET']).cumprod() for col in tickers}
df_trade = df_trade.assign(PF_RET=df_trade[ret_dict.keys()].dot(weights),
**cumret_dict,
PF_CUMRET=(1+df_trade[ret_dict.keys()].dot(weights)).cumprod())
cumret_cols = [col for col in df_trade.columns if 'CUMRET' in col]
# calculate MDD within the trading period
mdd_dict = {col.split('_')[0]+'_MDD': get_mdd(df_price=df_trade,
start=df_trade.index[0],
end=df_trade.index[-1],
col=col)
for col in cumret_cols}
df_trade = df_trade.assign(**mdd_dict)
return df_tradedf_res = pd.DataFrame()
for i in range(len(trading_period)):
df_trade = get_pf_returns(df_price=df,
tickers=tickers,
start=trading_period.iloc[i].start_date,
end=trading_period.iloc[i].end_date
)
df_res = pd.concat([df_res, df_trade], axis=0)
"""
drop duplicated rows of trading result dataframe
there are duplicated rows for each trading period except the first
"""
df_res = df_res.reset_index().drop_duplicates(['Date'], keep='first').set_index('Date')plt.rcParams.update(IPython_default);
plt.style.use('_mpl-gallery')
(1+df_res[['SPY_RET', 'TLT_RET', 'GLD_RET', 'CASH_RET', 'PF_RET']]).cumprod().plot(figsize=(12,8), linewidth=1);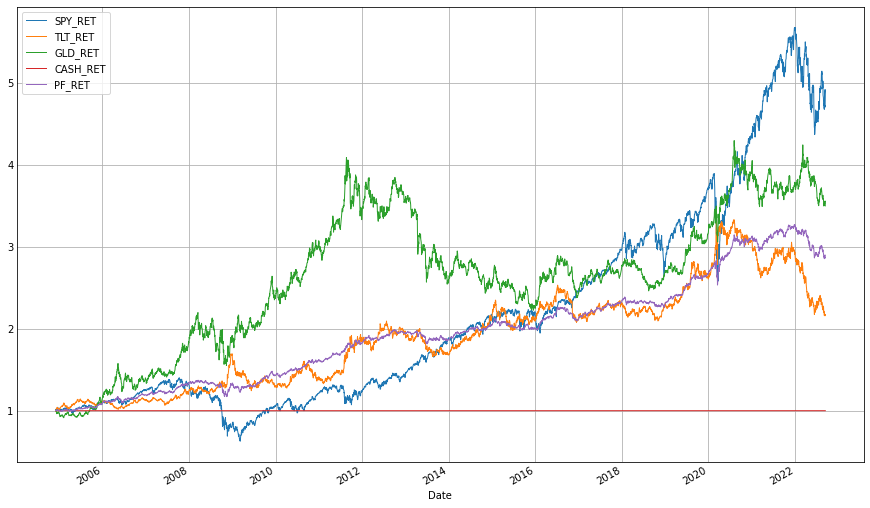
pf.show_perf_stats(returns=df_res.PF_RET)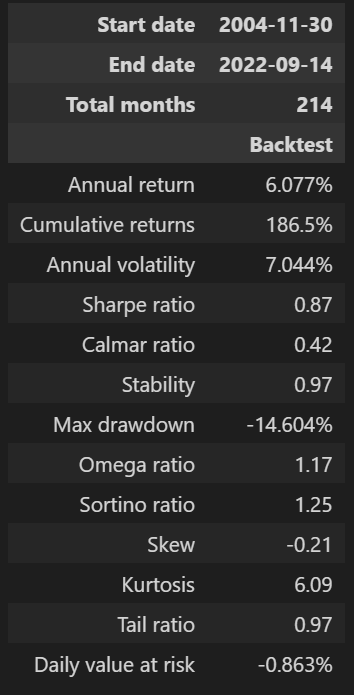
| 포트폴리오 | 초기자산 (달러) |
최종자산 (달러) |
연복리 수익률(%) |
표준편자 (%) |
수익 난 월 (%) |
MDD (%) |
샤프비율 |
| 영구 포트폴리오 |
10,000 | 762,322 | 8.8 | 7.2 | 65.0 | -12.7 | 0.57 |
이전 글에서 60/40 포트폴리오의 백테스팅 결과를 비교해보았을 때와 마찬가지로 연복리 수익률(Annual return)에서 차이가 크게 나타났다. MDD(Maximum drawdown)도 책에 제시된 값과 차이가 조금 있는데, 직접 구한 MDD의 절대값이 더 크게 나와서 이 부분은 이해가 잘 안 되긴 한다2.
MDD에 대한 설명은 아래 글 참고
- S&P, 나스닥 어디까지 왔나 - python으로 MDD(Maximum drawdown) 계산하기
pf.show_worst_drawdown_periods(returns=df_res.PF_RET, top=10)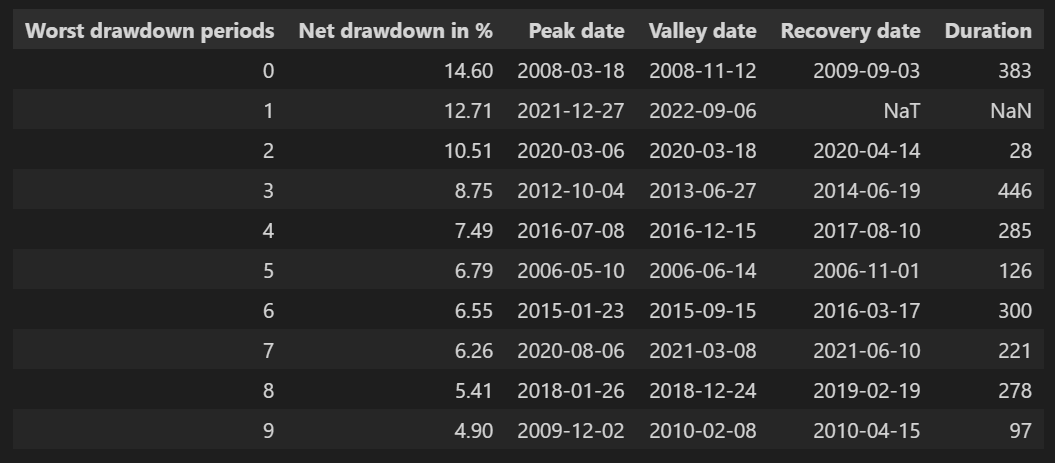
샤프비율(Sharpe ratio)도 값의 차이가 큰데, Allocate Smartly의 계산 방식이 어떻게 되는지 궁금하다3.
다음으로 60/40 포트폴리오를 벤치마크 포트폴리오로 하여 성과비교를 해보았다.
tickers = ['SPY', 'IEF']
df_res_6040 = pd.DataFrame()
for i in range(len(trading_period)):
df_trade = get_pf_returns(df_price=df_close[tickers].dropna(),
tickers=tickers,
start=trading_period.iloc[i].start_date,
end=trading_period.iloc[i].end_date
)
df_res_6040 = pd.concat([df_res_6040, df_trade], axis=0)
"""
drop duplicated rows of trading results dataframe
there are duplicated rows for each trading period except the first
"""
df_res_6040 = df_res_6040.reset_index().drop_duplicates(['Date'], keep='first').set_index('Date')
df_all = pd.concat([df_res.PF_RET, df_res_6040.PF_RET], keys=['Permanent', '60/40'], axis=1).dropna()
df_all_perf = pd.concat([pf.timeseries.perf_stats(returns=df_all['Permanent']),
pf.timeseries.perf_stats(returns=df_all['60/40'])
],
keys=['Permanent', '60/40'], axis=1)
round(df_all_perf.iloc[[0,1,2,3,6]]*100, 2)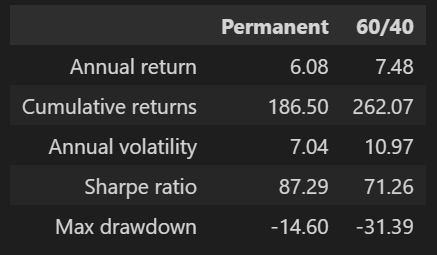
60/40 포트폴리오에 비해 영구 포트폴리오는
(1) 연율화 수익률(Annual return)은 작지만
(2) 상대적으로 수익률의 변동성(Annual volatility)이 작고,
(3) MDD(Max drawdown)는 반 이하로 감소한다.
'적게 벌지만 수익률이 상대적으로 안정적이고, 깨질 때 덜 깨진다' 정도로 바꿔 말할 수 있다.
plt.figure(figsize=(16,8))
plt.subplot(1, 2, 1)
pf.plot_annual_returns(returns=df_all['Permanent'])
plt.title(label='Permanent PF Annual returns')
plt.subplot(1, 2, 2)
pf.plot_annual_returns(returns=df_all['60/40'])
plt.title(label='60/40 PF Annual returns');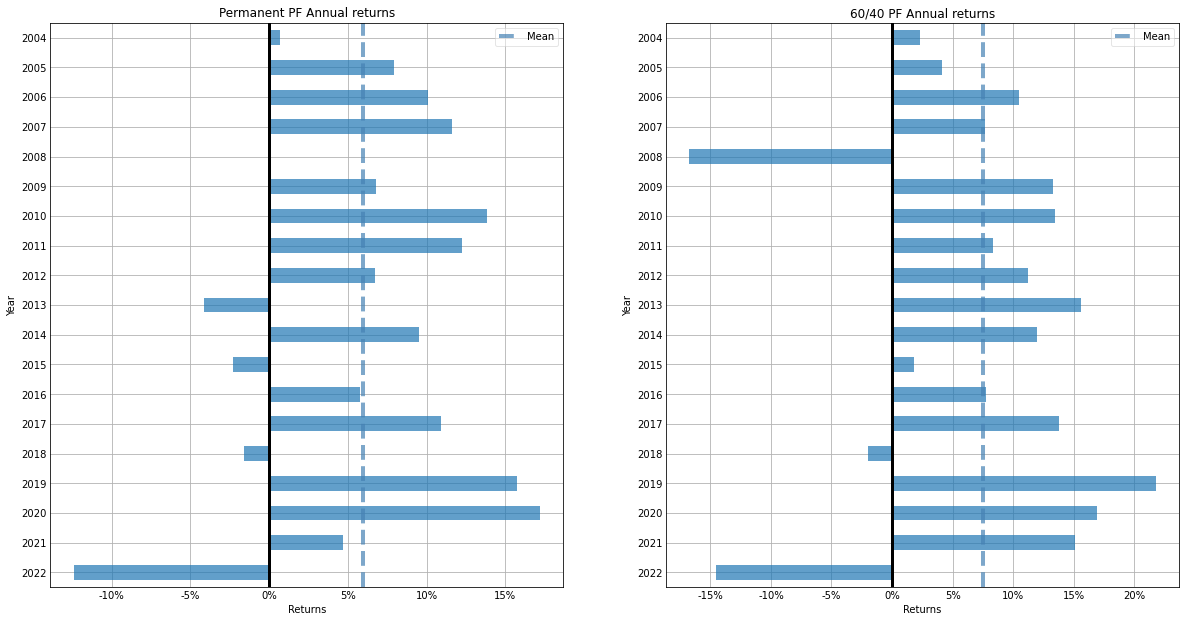
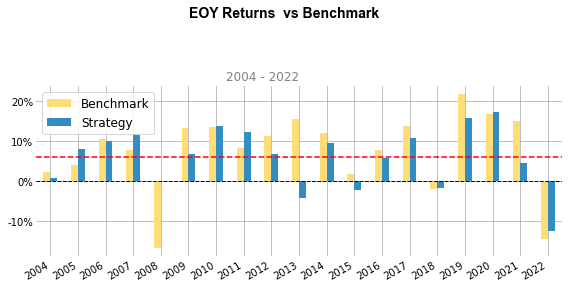
영구 포트폴리오와 60/40 포트폴리오의 연간 수익률을 비교해보면 2008년 금융위기 같은 시장 하락기에 잘 버티는 것을 볼 수 있다.
하지만 2013년, 2015년에는 60/40 포트폴리오는 플러스 수익률로 끝났는데, 영구 포트폴리오는 마이너스 수익률로 끝난 것을 볼 수 있다. 특히, 2013년에는 두 포트폴리오의 수익률 격차가 20% 가까이 나는 것을 볼 수 있다. 2013년에 영구 포트폴리오에 포함된 자산군들의 누적 수익률을 살펴보면
plt.rcParams.update(IPython_default);
plt.style.use('_mpl-gallery')
(1+df_res.loc['2013'][['SPY_RET', 'TLT_RET', 'GLD_RET', 'CASH_RET', 'PF_RET']]).cumprod().plot(figsize=(12,8), linewidth=1);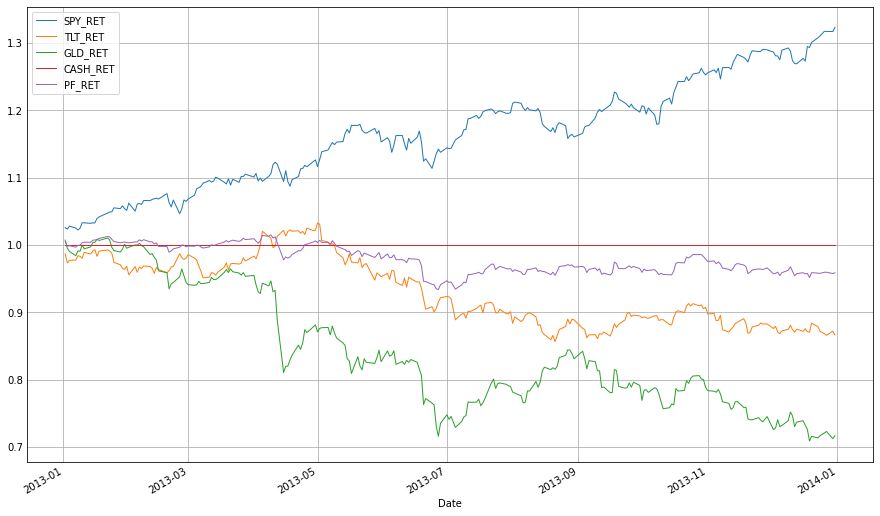
금(GLD)과 미국 채권(TLT)이 포트폴리오 수익률을 크게 갉아먹었다는 것을 알 수 있고, 특히 금의 퍼포먼스가 매우 좋지 않았다는 것을 알 수 있다. 2013년에 왜 금 가격이 크게 하락했을까 찾아보니 아래처럼 이유를 설명하고 있었다.
<[기획] 금값 2013년 들어 28% 폭락… 금 펀드도 덩달아 굴욕>
1년도 채 안돼 금값이 반전한 것은 (1) 미국의 양적완화 정책 종료 방침 때문이다. 금이 달러 등 기축통화 가치가 떨어질 때 대안제 역할을 했었는데 달러값이 오르면서 금 수요가 사라졌다.
또 (2) 미국 경제가 올여름 이후 눈에 띄는 회복세를 보이는 것도 금값 하락을 부채질하고 있다.
(3) 미국 국채금리가 오르고, (4) 안정세를 보이고 있는 유가도 금값을 떨어트리고 있다.
여기에 (5) 미국 증시 호황도 가세하고 있다.
2022년 현재의 상황에서 보면 (1), (3), (4)는 현재 상황에 해당되고, (2), (5)와는 반대되는 추세로 흘러가고 있다. 금이 2008년 금융위기 이후 2009~2012년까지 폭발적으로 상승했지만, 그 이후 움직임을 보면 전고점을 회복하기까지 8년의 기간이 필요했다(2020년이 되어서야 전고점 회복). 변동성이 큰 금의 움직임을 보면, 포트폴리오에서 금의 비중을 크게 가져 가는 것은 별로 좋지 않은 생각 같다.
포트폴리오의 성과를 확인할 때 사용할 수 있는 다른 패키지도 발견하여 실행해본 결과를 첨부한다. quantstats라는 패키지인데, pyfolio에 비해 좀 더 다양한 성과지표를 계산해주고, 결과물의 포맷이 좀 더 깔끔하게 정리되어 나온다. html 파일로 결과 보고서를 저장할 수 있는 함수(qs.reports.html)도 존재한다.
qs.reports.full(returns=df_all['Permanent'], benchmark=df_all['60/40'])Performance Metrics
Strategy Benchmark
------------------------- ---------- -----------
Start Period 2004-11-30 2004-11-30
End Period 2022-09-14 2022-09-14
Risk-Free Rate 0.0% 0.0%
Time in Market 100.0% 100.0%
Cumulative Return 186.5% 262.07%
CAGR﹪ 6.09% 7.5%
Sharpe 0.87 0.71
Prob. Sharpe Ratio 99.99% 99.86%
Smart Sharpe 0.86 0.7
Sortino 1.25 1.01
Smart Sortino 1.23 0.99
Sortino/√2 0.88 0.71
Smart Sortino/√2 0.87 0.7
Omega 1.17 1.17
Max Drawdown -14.6% -31.39%
Longest DD Days 622 1014
Volatility (ann.) 7.04% 10.97%
R^2 0.4 0.4
Information Ratio -0.01 -0.01
Calmar 0.42 0.24
Skew -0.21 0.01
Kurtosis 6.1 15.68
Expected Daily % 0.02% 0.03%
Expected Monthly % 0.49% 0.6%
Expected Yearly % 5.7% 7.01%
Kelly Criterion 4.66% 5.12%
Risk of Ruin 0.0% 0.0%
Daily Value-at-Risk -0.71% -1.11%
Expected Shortfall (cVaR) -0.71% -1.11%
Max Consecutive Wins 11 16
Max Consecutive Losses 10 10
Gain/Pain Ratio 0.17 0.15
Gain/Pain (1M) 1.03 1.01
Payoff Ratio 0.92 0.88
Profit Factor 1.17 1.15
Common Sense Ratio 1.14 1.1
CPC Index 0.58 0.56
Tail Ratio 0.97 0.96
Outlier Win Ratio 4.59 3.38
Outlier Loss Ratio 5.0 3.48
MTD -1.03% -0.78%
3M -0.57% 3.75%
6M -9.61% -6.76%
YTD -12.42% -14.55%
1Y -10.39% -11.37%
3Y (ann.) 3.19% 6.65%
5Y (ann.) 4.54% 7.26%
10Y (ann.) 3.78% 8.2%
All-time (ann.) 6.09% 7.5%
Best Day 3.11% 8.44%
Worst Day -3.23% -5.72%
Best Month 5.76% 7.76%
Worst Month -8.14% -9.77%
Best Year 17.2% 21.77%
Worst Year -12.42% -16.73%
Avg. Drawdown -1.06% -1.06%
Avg. Drawdown Days 27 17
Recovery Factor 12.77 8.35
Ulcer Index 0.03 0.06
Serenity Index 4.06 2.81
Avg. Up Month 1.81% 2.25%
Avg. Down Month -1.7% -2.52%
Win Days % 54.44% 55.52%
Win Month % 59.81% 67.76%
Win Quarter % 73.61% 75.0%
Win Year % 78.95% 84.21%
Beta 0.41 -
Alpha 0.03 -
Correlation 63.16% -
Treynor Ratio 459.64% -5 Worst Drawdowns
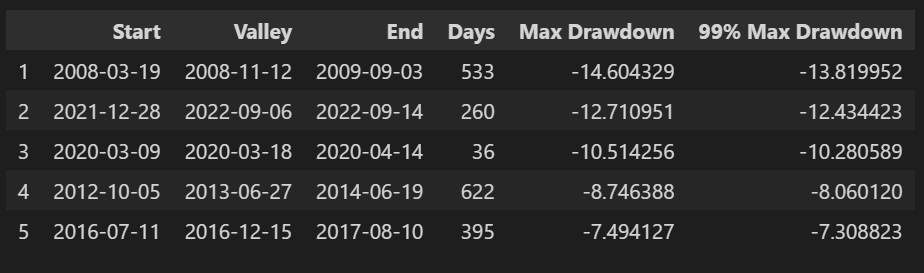
Strategy Visualization
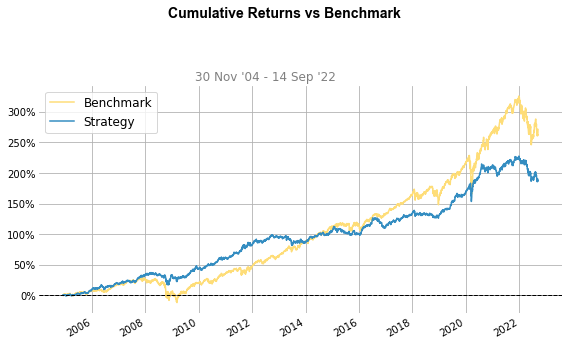
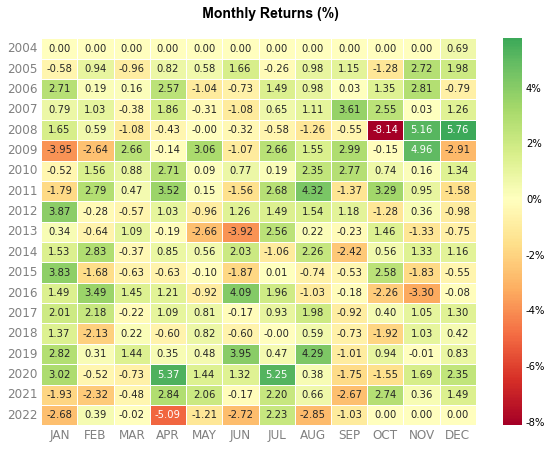
영구 포트폴리오의 연도별x월별 수익률 히트맵을 보면 2008년에 10월에는 큰 하락을 겪었지만 11월 12월에 하락분을 모두 회복하는 상승을 보이는데 어떤 자산군에서 상승이 있었는지 살펴보자.
plt.rcParams.update(IPython_default);
plt.style.use('_mpl-gallery')
(1+df_res.loc['2008'][['SPY_RET', 'TLT_RET', 'GLD_RET', 'CASH_RET', 'PF_RET']]).cumprod().plot(figsize=(12,8), linewidth=1);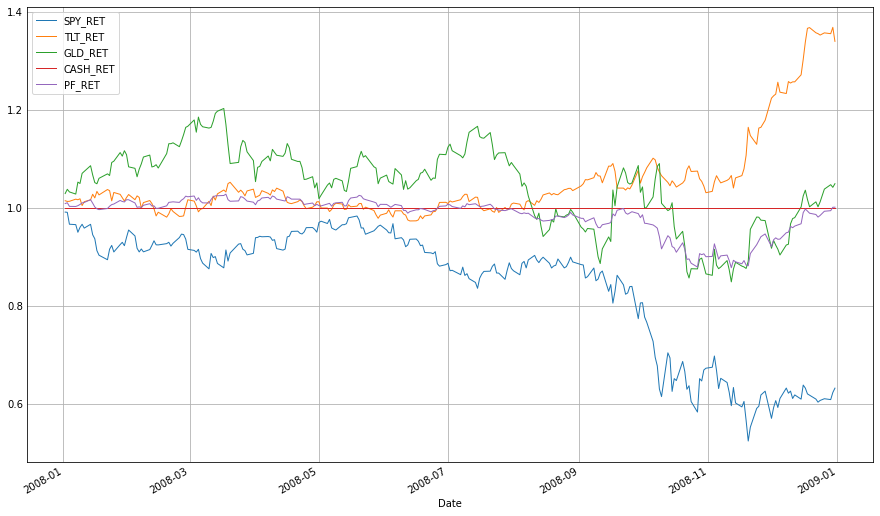
미국 주식(SPY)은 2008년 9월 이후 크게 박살 났지만 미국 채권(TLT)이 2008년 11월 이후 크게 상승하면서 이를 상쇄한 것으로 보인다.
3. 글을 마치며
이번 글에서는 영구 포트폴리오의 백테스팅 결과를 60/40 포트폴리오와 비교해보면서 특정 시기에 어떤 자산군이 포트폴리오 수익률에 어떤 영향을 주었는지 살펴보았다. 데이터를 보면서 느꼈던 점 중 하나는 금을 포트폴리오에 포함시키는 게 정말 도움이 되는 것인지 잘 모르겠다는 것이다.

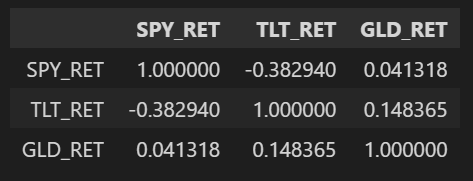
금이 다른 자산군과의 상관성이 낮긴 하지만, 우상향 하는 자산이라고 보기에는 2013년~2020년까지의 하락구간이 너무 길었고, 수익률의 변동성이 너무 큰 게 아닌가 하는 생각이 든다. 금은 Buy and Hold 전략으로 가져가기 보다는 마켓타이밍 전략4을 적절히 섞는 게 어떨까 하는 생각이 드는데, 이건 좀 더 데이터를 봐야 할 것 같다.
그리고 1970년대~1990년대 데이터를 각 ETF의 벤치마크 인덱스와 비교해서 만들어봐야겠다는 생각을 다시 한번 해보게 되었다5. ETF들의 상장시기가 2000년대 이후인 경우가 많아서 전략들이 오일쇼크나 닷컴 버블 같은 극단적인 스트레스 상황에서 얼마나 잘 버티는지 확인해보는데 한계가 큰 것 같다.
4. 참고자료
강환국, 『거인의 포트폴리오』, page2-(2021), p.163-p.167
- 1996년, 2000년에 미국 자유당(Libertarian Party) 대선 후보로 출마 했다. [본문으로]
- MDD의 절대값이 더 작게 나왔다면 1970년 1월~2004년 11월에 그 값이 나왔을 것이라고 추측해볼 수 있지만 반대의 경우는 발생할 수 없기 때문 [본문으로]
- 웹사이트에서 정확히 어떤 수식으로 계산하는지 설명이 없어서 제대로 확인해보지는 못했다. [본문으로]
- 예를 들어, 리밸런싱 일자에 200일 이동평균선 위에 있을 때만 매수 아니면 매도 [본문으로]
- 벤치마크 인덱스 데이터를 좀 찾아봤는데 IET, TLT 등 국채관련 ETF의 벤치마크 인덱스의 ETF 상장 이전 과거 데이터를 제공하는 곳을 아직까지 찾지 못했다. [본문으로]