[백테스팅] 정적자산배분 - (1) 유대인 전략
관련 글 목록
1. 들어가며
import yfinance as yf
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
IPython_default = plt.rcParams.copy()
import matplotlib.dates as mdates
plt.style.use('tableau-colorblind10')
df_SPY = yf.Ticker('SPY').history('max', auto_adjust=True)
historical_high_date = df_SPY.iloc[df_SPY.Close.argmax()].name.strftime('%Y-%m-%d')
df_SPY.Close.plot(figsize=(16,8))
plt.title('SPY Close')
plt.axvline(x=historical_high_date, color='green', linestyle='dashed')
plt.text(x=historical_high_date, y=500, s=historical_high_date);
올해 초 S&P500이 역사적 고점을 여러 번 갱신한 이후 주식시장의 변동성이 심해지고 있다.
df_ret = df_SPY.loc['2020-12-31':'2022-08-31', 'Close'].pct_change().dropna()
df_ret.index = df_ret.index.strftime('%y/%m/%d')
fig, ax = plt.subplots(figsize=(20,8))
ax = df_ret.plot.bar(color=(df_ret>0).map({True: 'g', False: 'r'}))
ax.xaxis.set_major_locator(mdates.MonthLocator(interval=1))
plt.title('SPY Daily Return (2021.1~2022.8)')
plt.axhline(y=0.01, linestyle='dashed')
plt.axhline(y=-0.01, linestyle='dashed')
plt.xticks(fontsize=7)
plt.ylabel('Daily Return');
변동성이 심한 환경일수록 자산배분을 통해 리스크를 줄이는 것이 중요하다는 생각이 들어 관련 내용을 공부하는 중이다. 이번 글에서는 '거인의 포트폴리오'라는 책에 소개된 자산배분의 3대 원칙에 대해 간단히 정리한 후, 정적자산배분 전략 중 첫번째로 제시된 유대인 전략을 살펴보고자 한다.
거인의 포트폴리오 - YES24
돈 버는 사람들은 이렇게 주식을 삽니다!따라만 하면 수익이 나는 대가들의 검증된 투자 시스템주식, 코인, 부동산 무엇에 투자했든 “그때 살걸!” 혹은 “그때 팔걸!”이라고 생각해 보지 않
www.yes24.com
2. 자산배분의 3대 원칙
1. 장기적으로 우상향 하는 자산군을 보유한다.
2. 상관성이 낮은 자산군을 보유한다.
3. 자산군별 변동성을 비슷하게 유지한다.
거인의 포트폴리오(강환국) p.126-p.133
개별 자산배분 전략으로 들어가기 전에 책에 소개된 자산배분의 3대 원칙을 살펴보자.
2.1. 장기적으로 우상향 하는 자산군을 보유한다.
자산배분은 기본적으로 여러 자산들은 '보유'하는 것이기 때문에 장기적 관점에서 볼 때 최소한 물가상승률 이상의 상승률을 보이는 자산이 그 대상이 되어야 한다. 책에서는 두 가지 레퍼런스를 참고하여 부동산, 주식, 채권, 현금, 금, 원자재를 자산배분의 대상으로 제시하고 있다.
2.2. 상관성이 낮은 자산군을 보유한다.
항상 같은 방향으로 움직이는 자산군에만 자산배분을 한다면 위기 상황에서 하방 리스크를 줄이는데 큰 도움이 되지 않을 것이다. 특정 경제상황에서 서로 다른 방향으로 움직이는 자산군을 보유했을 때 포트폴리오 전체의 리스크를 줄일 수 있기 때문에 자산배분은 상관성이 낮은1 자산군을 대상으로 하는 것이 좋다.
2.3. 자산군별 변동성을 비슷하게 유지한다.
포트폴리오에 포함된 자산군별 변동성이 크게 차이 난다면, 변동성이 큰 특정 자산군에서 큰 하락이 발생했을 때, 상관성이 낮은 다른 자산군이 상승한다고 해도, 포트폴리오 전체 수익률을 방어하지 못하게 될 가능성이 있다. 자산군별 변동성을 비슷하게 유지하는 방법을 리스크 패리티(Risk Parity)라고 하며 레이달리오의 올웨더 펀드가 리스크 패리티 개념을 적용하여 운용하는 대표적인 사례이다.
3. 정적자산배분
책에서는 자산배분의 유형을 '정적자산배분(Static Asset Allocation)'과 '동적자산배분(Dynamic Asset Allocation)'으로 나누어 설명하고 있다. 정적자산배분이 일반적으로 알려진 자산배분 방식을 뜻하며, 동적자산배분은 자산배분에 마켓타이밍 기법이 적용된 방법이라고 한다. 동적자산배분은 전술적자산배분(Tactical Asset Allocation)이라고 표현하는 경우도 있다고 한다. 이번 글에서는 정적자산배분 기법으로 소개된 전략 중 유대인 전략에 대한 백테스팅 과정과 결과를 적어보았다.
3.1. 유대인 전략
거인의 포트폴리오(강환국) p.139-p.143
탈무드에 전해지는 아래와 같은 내용을 바탕으로 만들어진 전략이라고 한다.
자산을 3등분하여 1/3은 토지에 1/3은 사업에 투자하고, 나머지 1/3은 여유자금으로 가지고 있어라.
부동산, 주식, 현금으로 자산을 3등분 하라는 뜻이고, 현금 대신 안정성이 높고 어느 정도 수익이 나오는 장기국채를 포함할 수 있다.
| 투자전략 | 유대인 전략 |
| 기대 연복리수익률 | 10% 전후 |
| 포함자산 | 미국주식(SPY), 미국 장기국채(TLT), 미국 리츠(VNQ) |
| 매수전략 | 3개 ETF에 자산을 3등분 |
| 매도전략 | 연 1회 리밸런싱 |
| 포트폴리오 | 초기자산 (달러) |
최종자산 (달러) |
연복리 수익률(%) |
표준편자 (%) |
최고의 해 (%) |
최악의 해 (%) |
MDD (%) |
샤프 비율 |
| 유대인 전략 |
10,000 | 134,456 | 9.85 | 10.00 | 26.59 | -16.79 | -36.95 | 0.76 |
유대인 전략의 주요 지표(1994.1~2021.8)
개인이 수집 가능한 데이터로 책에서 제시된 성과 지표들이 실제로 나오는 값인지 확인해보자. 데이터는 야후 파이낸스 데이터를 가져오는 yfinance 패키지를 이용하였다. yfinance 사용법이 궁금하다면 아래 글을 참고.
- [ML4T] 미국 주식 데이터 수집하기 - 주가, 거래량, 재무 데이터
- [ML4T] S&P500 종목의 백테스트와 주가 수익률 예측을 위한 데이터셋 만들기 - yfinance, talib
import yfinance as yf
import pandas as pd
tickers = ['SPY', 'TLT', 'VNQ']
weights = [1/len(tickers) for _ in range(len(tickers))]
df_close = yf.download(tickers=tickers,
period='max',
interval='1d',
auto_adjust=True # True: adjust all OHLC automatically
)['Close'][tickers]SPY, TLT, VNQ의 종가 데이터를 가져온 후 각 데이터의 시작일자를 확인해보았다.
print('Start date of each stock')
print('-'*25)
for ticker in tickers:
print(f"{ticker}: {df_close[[ticker]].dropna().iloc[0].name.strftime('%Y-%m-%d')}")
print('-'*25)
Start date of each stock
-------------------------
SPY: 1993-01-29
TLT: 2002-07-30
VNQ: 2004-09-29
-------------------------TLT는 2002년 7월 30일, VNQ는 2004년 9월 29일부터 데이터가 있는데 책에 제시된 백테스트 기간은 1994년 1월~2021년 8월이다. 책에서 사용한 자료는 Allocate Smartly라는 웹사이트에서 가져온 것으로 이 웹사이트의 설명을 보면 특정 ETF가 상장되지 않은 기간 동안의 데이터는 해당 ETF가 추종하는 인덱스를 기반으로 시뮬레이션 된 데이터를 사용했다고 한다.
Simulated Asset Data
In order to extend our backtests as far into the past as possible, we often make use of simulated data.
For example, a strategy trading the S&P 500 ETF SPY could only be tested back to 1993, when SPY began trading, using actual data. But using alternate data sources, such as the underlying index on which the ETF is based, we’re able to extend that data much further into the past.
This is inappropriate for hyperactive strategies that rely on small price changes to generate return, because this simulated data is not sufficiently accurate. It is also inappropriate for very illiquid assets where, had traders actually been trading the asset, it would have significantly moved the price. In our case, neither is true. The strategies that we track are relatively slow moving, capturing broad trends rather than quickly capturing small price changes. And the assets those strategies trade tend to be very broad in nature, like stock indices, bond indices, or gold.
In short, we believe that the benefit of having more data to consider far outweighs the potential drawbacks of using simulated data.
Note that when creating simulated data, we apply an expense ratio equal to that of the most liquid similar ETF. So for example, when simulating data for an S&P 500 ETF, we apply the same expense ratio as SPY, the most liquid ETF in that space.
Also note that we tend to be much stricter when simulating asset data than you’ll see elsewhere. We discuss this issue further on our blog: The Perils of Backtesting with Unrealistic Data
트레이딩 일자는 데이터가 존재하는 2004년 9월의 마지막 영업일인 2004년 9월 30일부터 시작하도록 하였고, 그 이후로는 1년 단위 리밸런싱을 위한 트레이딩 기간을 잡아주었다.
df = df_close.dropna()
"""
define trading period
time_period: dataframe converted from datetime index of price dataframe
traiding_period: dataframe contains start_date and end_date of trading
+ resampled from time_period to yearly frequency and last business day of a month
+ last day of time_period assigned to last end_date
"""
time_period = df.index.to_frame()
trading_period = time_period.resample('BM').last().iloc[::12, :].rename(columns={'Date':'start_date'})
trading_period = trading_period.assign(end_date=trading_period.start_date.shift(-1).fillna(time_period.iloc[-1].name))
trading_period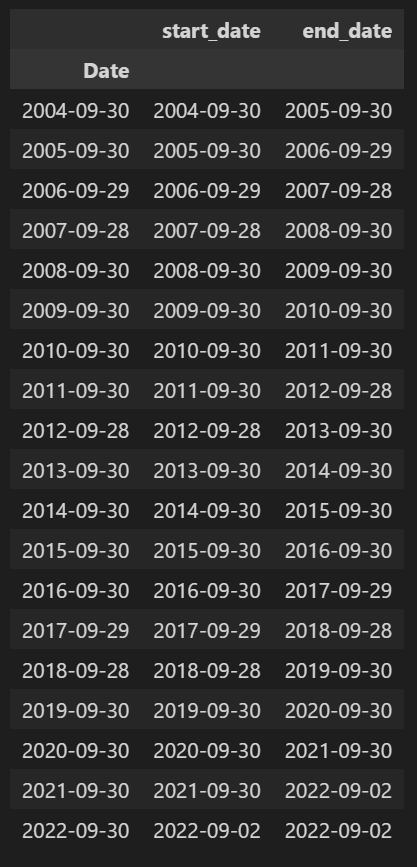
다음은 추후에 작성할 동적자산배분 전략 백테스팅에서도 사용하기 위해 필요한 기능들을 몇 가지 구현한 코드이다. 이번 글에서는 포트폴리오의 일별 수익률을 계산한 결과만 사용하였다.
def get_mdd(df_price, start, end, col):
"""
generates maximum drawdown(MDD) of asset prices
MDD: the maximum observed loss from a peak to a trough of a portfolio, before a new peak is attained
Parameters
----------
df_price: pd.DataFrame
dataFrame with datetime index and (adjusted) close prices
example:
----------------------------------------------------
SPY IEF
Date
2002-07-30 61.6628 46.0411
2002-07-31 61.8120 46.4633
... ... ...
2022-09-15 388.5240 98.6000
2022-09-16 385.5600 98.6800
----------------------------------------------------
start: datetime
trading start date
example: Timestamp('2004-11-30 00:00:00')
end: datetime
trading end date
example: Timestamp('2005-11-30 00:00:00')
col: str
The column name of the cumulative return of the asset for which MDD is to be calculated
Return
----------
return: pd.Series
Series of MDD for the trading period
"""
# select data within the trading period
df_price = df_price[start:end].copy()
return ((df_price[col]-df_price[col].cummax())/df_price[col].cummax()).cummin()
def get_pf_returns(df_price, tickers, start, end, weights=None, use_signal=None):
"""
generates portfolio returns
Parameters
----------
df_price: pd.DataFrame
dataFrame with datetime index and (adjusted) close prices
example:
----------------------------------------------------
SPY IEF
Date
2002-07-30 61.6628 46.0411
2002-07-31 61.8120 46.4633
... ... ...
2022-09-15 388.5240 98.6000
2022-09-16 385.5600 98.6800
----------------------------------------------------
tickers: list
list of tickers
example: ['SPY', 'IEF']
start: datetime
trading start date
example: Timestamp('2004-11-30 00:00:00')
end: datetime
trading end date
example: Timestamp('2005-11-30 00:00:00')
weights: list, optional
list of weights. if weights is None, equal weights are assumed
example: [0.6, 0.4]
use_signal: Boolean, optional
True/False. if True is assigned, buy signal is used. #### future work
Return
----------
return: pd.DataFrame
prices, daily returns, cumulative returns, MDD for each asset and the portfolio
example:
----------------------------------------------------
SPY IEF SPY_RET IEF_RET PF_RET SPY_CUMRET IEF_CUMRET PF_CUMRET SPY_MDD IEF_MDD PF_MDD
Date
2002-07-31 0.0000 0.0000 0.0000 0.0000 0.0000 1.0000 1.0000 1.0000 0.0000 0.0000 0.0000
2002-08-01 60.1982 46.6548 -0.0261 0.0041 -0.0110 0.9739 1.0041 0.9890 -0.0261 0.0000 -0.0110
2002-08-02 58.8489 47.0152 -0.0224 0.0077 -0.0073 0.9521 1.0119 0.9817 -0.0479 0.0000 -0.0183
... ... ... ... ... ... ... ... ... ... ... ...
2003-07-30 68.3896 49.3867 -0.0024 0.0080 0.0028 1.1064 1.0629 1.0959 -0.1886 -0.0743 -0.0733
2003-07-31 68.5482 49.0572 0.0023 -0.0067 -0.0022 1.1090 1.0558 1.0936 -0.1886 -0.0743 -0.0733
----------------------------------------------------
"""
# define weights
if weights is None:
weights = [1/len(tickers) for _ in range(len(tickers))]
# calculate daily returns
ret_dict = {f'{ticker}'+'_RET': df_price[ticker].pct_change().fillna(0) for ticker in tickers}
df_price = df_price.assign(**ret_dict)
# select data within the trading period
df_trade = df_price.loc[start:end].copy()
# assign 0 for the first row. returns cannot be calculated on the first trading day
df_trade.loc[start, :] = 0
#### future work
"""
if use_signal==True:
df_sig = pd.concat([df_trade.index.to_frame().drop(columns=['Date']),
df.loc[[start], sig_dict.keys()]
], axis=1).ffill()
df_sig.columns = tickers
df_trade = df_trade.assign(**{col: df_trade[col]*df_sig[col] for col in tickers})
else:
df_trade = df_trade.assign(**{col: df_trade[col] for col in tickers})
"""
# calculate daily portfolio returns
df_trade = df_trade.assign(PF_RET=df_trade[ret_dict.keys()].dot(weights))
# calculate cumulative returns within the trading period
cumret_dict = {f'{col}_CUMRET': (1+df_trade[f'{col}_RET']).cumprod() for col in tickers}
df_trade = df_trade.assign(PF_RET=df_trade[ret_dict.keys()].dot(weights),
**cumret_dict,
PF_CUMRET=(1+df_trade[ret_dict.keys()].dot(weights)).cumprod())
cumret_cols = [col for col in df_trade.columns if 'CUMRET' in col]
# calculate MDD within the trading period
mdd_dict = {col.split('_')[0]+'_MDD': get_mdd(df_price=df_trade,
start=df_trade.index[0],
end=df_trade.index[-1],
col=col)
for col in cumret_cols}
df_trade = df_trade.assign(**mdd_dict)
return df_tradedf_res = pd.DataFrame()
for i in range(len(trading_period)):
df_trade = get_pf_returns(df_price=df,
tickers=tickers,
start=trading_period.iloc[i].start_date,
end=trading_period.iloc[i].end_date
)
df_res = pd.concat([df_res, df_trade], axis=0)
"""
drop duplicated rows of trading result dataframe
there are duplicated rows for each trading period except the first
"""
df_res = df_res.reset_index().drop_duplicates(['Date'], keep='first').set_index('Date')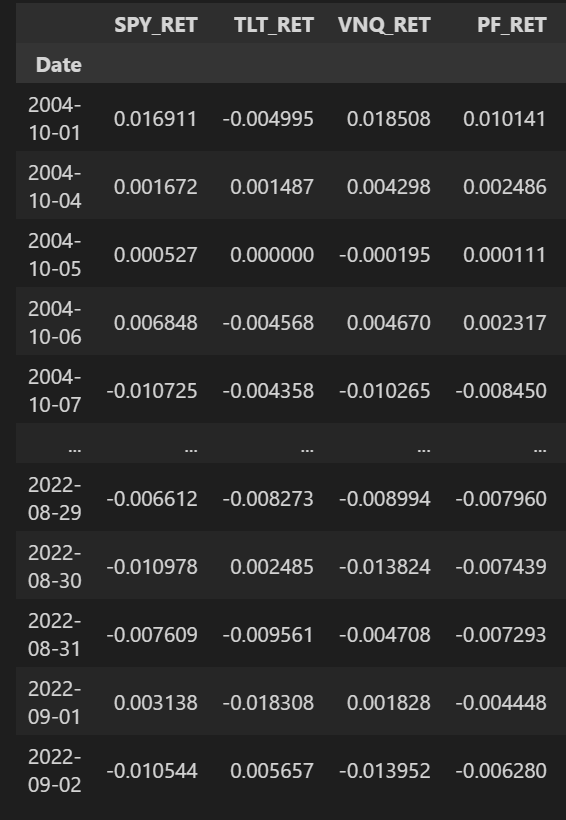
포트폴리오 성과 분석은 pyfolio 패키지의 create_returns_tear_sheet 함수를 이용하면 간단하게 수행할 수 있다. 함수에 포트폴리오의 일별 수익률과 벤치마크 수익률을 넣어주면 성과 분석표와 각종 그래프들을 뽑아주는데 이 글에는 성과분석표만 첨부한다.
import pyfolio as pf
pf.create_returns_tear_sheet(returns=df_res.PF_RET, benchmark_rets=df_res.SPY_RET)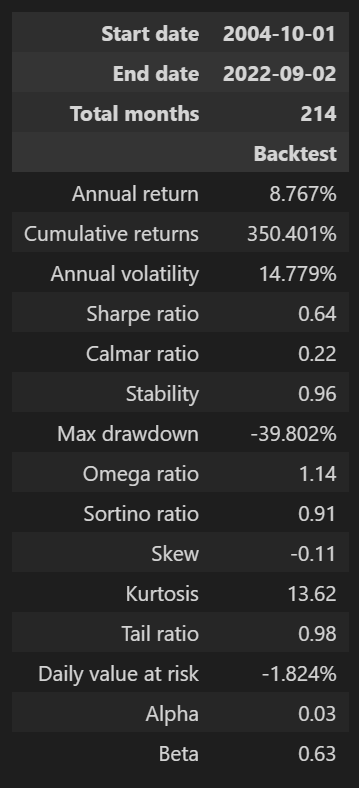
| 포트폴리오 | 초기자산 (달러) |
최종자산 (달러) |
연복리 수익률(%) |
표준편자 (%) |
최고의 해 (%) |
최악의 해 (%) |
MDD (%) |
샤프 비율 |
| 유대인 전략 |
10,000 | 134,456 | 9.85 | 10.00 | 26.59 | -16.79 | -36.95 | 0.76 |
연복리수익률(Annual return)이 책에 제시된 값보다 1%p 정도 낮은 8.767%로 나왔고, MDD는 조금 더 좋지 않은 -39.802%로 나왔다. 샤프 비율(Sharp ratio)은 책에 제시된 값보다 더 낮은 0.64가 나왔고, 표준편차(Annual volatility)는 더 높은 14.779%가 나왔다. 전체적으로 보았을 때, 책에 제시된 결과에 비해 좀 더 좋지 않은 결과가 나왔다. 책에 제시된 결과는 1994년부터 2003년까지 기간 동안의 백테스팅 결과도 포함된 것인데, 이 기간동안 유대인 전략의 수익률이 그 이후 기간 대비 더 좋았다는 것을 추측해볼 수 있다.
유대인 전략이 글의 전반부에서 언급한 자산배분은 3대 원칙에 부합하는지도 살펴보자.
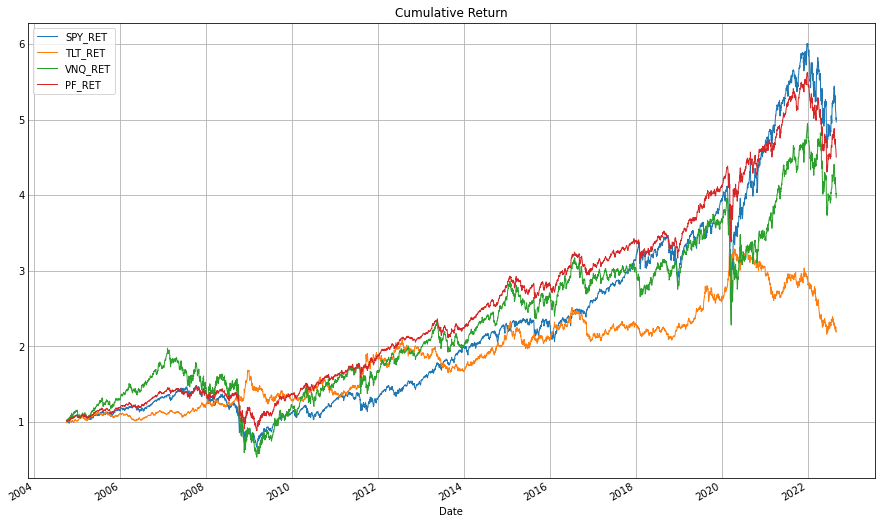
먼저 SPY, TLT, VNQ가 우상향하는 자산이 맞는지 보면, 정도의 차이는 있지만 모두 가치가 상승한 자산이라고 할 수 있다.
두 번째로 자산간의 상관성이 어느 정도인지 살펴보자.
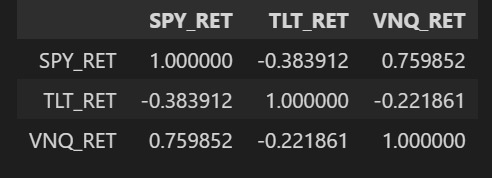
세 ETF의 일별 수익률의 상관계수를 구해보면 SPY와 VNQ의 일별 수익률 간 상관계수는 높게 나타나지만, SPY와 TLT, VNQ와 TLT의 일별 수익률은 음의 상관계수를 보여 반대방향으로 움직이는 자산이라는 것을 알 수 있다.
마지막으로 변동성이 비슷한 자산인지 살펴보자. 변동성은 pyfolio의 create_return_tear_sheet 함수를 통해 구할 수 있는 Annual volatility(연율화 표준편차) 기준으로 살펴보았다.
| 자산 | Annual volatility |
| SPY | 19.385% |
| TLT | 14.37% |
| VNQ | 30.059% |
VNQ의 변동성이 SPY나 TLT에 비해 변동성이 큰 것을 볼 수 있고, 세번째 원칙에 따르려면 자산별 가중치를 변동성에 따라 다르게(변동성이 큰 자산의 비중은 작게, 변동성이 작은 자산의 비중은 크게) 가져가야 하지만 유대인 전략은 동일가중 포트폴리오 전략이기 때문이 세번째 원칙은 지켜지지 않은 것으로 볼 수 있다.
4. 글을 마치며
이번 글에서는 정적자산배분이 무엇인지와 자산배분의 3대 원칙에 대해 간략하게 정리해보았고, 정적자산배분 전략 중 하나로 거인의 포트폴리오에 소개된 유대인 전략에 대한 백테스팅을 진행해보았다. 다음 글부터는 책에 제시된 다른 정적자산배분 전략들에 대한 백테스팅 결과를 책에 나온 결과와 비교해보는 글들을 작성하게 될 것 같다.
5. 참고자료
강환국, 『거인의 포트폴리오』, page2-(2021), p.126-p.133, p.139-p.143
- 여기서 '상관성이 낮다'는 표현은 '두 자산의 수익률이 반대방향으로 움직인다'='음의 방향으로 갈 수록 두 자산의 상관성이 낮다'로 이해하는게 맞을 것 같다. [본문으로]